mirror/cube-studio
2
0
Fork 0
mirror of https://github.com/tencentmusic/cube-studio.git synced 2024-11-27 05:33:10 +08:00
Code Issues Packages Projects Releases Wiki Activity

Merge branch 'master' of https://github.com/tencentmusic/cube-studio

Browse Source
This commit is contained in:
cdllp2 2022-09-21 10:32:48 +08:00
commit eb7959c60d
11 changed files with 3540 additions and 0 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

209
aihub/machine-learning/BIRCH聚类.ipynb Normal file
View File

@ -0,0 +1,209 @@
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 1. BIRCH概述\n",
"\n",
"\n",
"　　　　BIRCH的全称是利用层次方法的平衡迭代规约和聚类（Balanced Iterative Reducing and Clustering Using Hierarchies），名字实在是太长了，不过没关系，其实只要明白它是用层次方法来聚类和规约数据就可以了。\n",
" \n",
" 刚才提到了，BIRCH只需要单遍扫描数据集就能进行聚类，那它是怎么做到的呢？\n",
"\n",
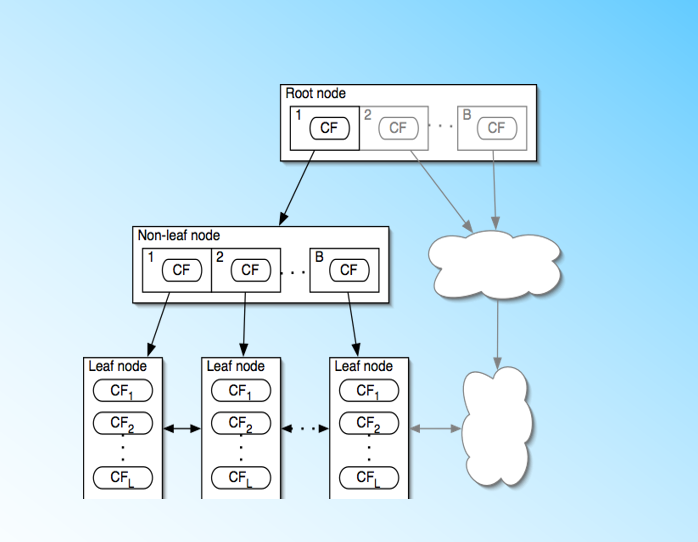
"　　　　BIRCH算法利用了一个树结构来帮助我们快速的聚类，这个数结构类似于平衡B+树，一般将它称之为聚类特征树(Clustering Feature Tree，简称CF Tree)。这颗树的每一个节点是由若干个聚类特征(Clustering Feature，简称CF)组成。\n",
" \n",
" 从下图我们可以看看聚类特征树是什么样子的：树中的每个节点（包括叶子节点）都有若干个CF，而内部节点的CF有指向孩子节点的指针，所有的叶子节点用一个双向链表链接起来。\n",
"\n",
"![这里写图片描述](https://img-blog.csdnimg.cn/img_convert/4ee6dab6703a913292b0b39e8e727ebf.png)\n",
"\n",
"\n",
"　　　　有了聚类特征树的概念，我们再对聚类特征树和其中节点的聚类特征CF做进一步的讲解。\n",
" \n",
"　　　　\n",
"**树中的每个节点都对应一个簇（或者叫聚类）。子节点对应的簇是父节点对应的簇的子簇，所以BIRCH算法算是基于层次的聚类算法。**"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 2. 聚类特征CF与聚类特征树CF Tree\n",
"\n",
"\n",
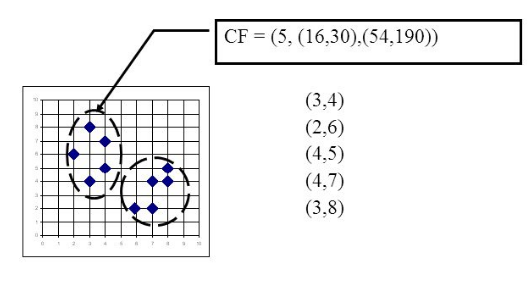
" 　　　　在聚类特征树中，一个节点的聚类特征CF是这样定义的：每一个CF是一个三元组，可以用（N，LS，SS）表示。其中N代表了这个簇中拥有的样本点的数量，这个好理解；LS代表了这个簇中拥有的样本点各特征维度的和向量，SS代表了这个簇中拥有的样本点各特征维度的平方和。\n",
" \n",
" 举个例子如下图，在CF Tree中的某一个节点对应的簇中，有下面5个样本(3,4), (2,6), (4,5), (4,7), (3,8)。则它对应的N=5， LS=(3+2+4+4+3,4+6+5+7+8)=(16,30), SS =(32+22+42+42+32+42+62+52+72+82)=(54+190)=244\n",
"\n",
"![这里写图片描述](https://img-blog.csdnimg.cn/img_convert/0175b472654f6c1bb0d5bea950e66c29.png)\n",
"\n",
"　　　　CF有一个很好的性质，就是满足线性关系，也就是CF1+CF2=(N1+N2,LS1+LS2,SS1+SS2)。这个性质从定义也很好理解。\n",
" \n",
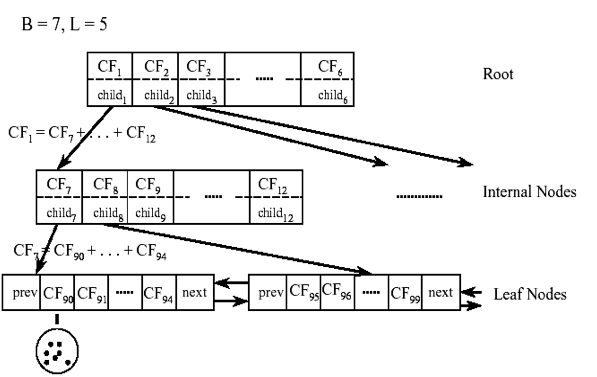
" 如果把这个性质放在CF Tree上，也就是说，在CF Tree中，对于每个父节点中的CF，它的(N,LS,SS)三元组的值等于它的子节点的三元组之和。如下图所示：\n",
"\n",
"![这里写图片描述](https://img-blog.csdnimg.cn/img_convert/5d6efeb14a1e49f5736ce71fd8601417.png)\n",
"\n",
"　　　　从上图中可以看出，根节点的CF1的三元组的值，可以从它指向的6个子节点（CF7 - CF12）的值相加得到。这样我们在更新CF Tree的时候，可以很高效。\n",
"\n",
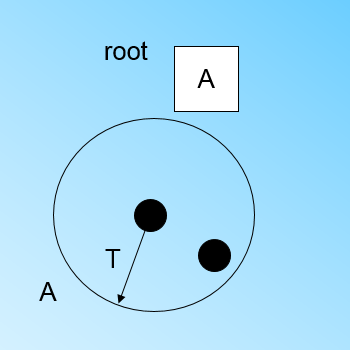
"　　　　对于CF Tree，我们一般有几个重要参数，第一个参数是分支因子B，表示每个非叶节点的子女的最大数目，第二个参数是阈值T，表示存储在树的叶节点中的子簇的最大直径。\n",
" \n",
" 也就是说，叶节点对应的子簇中的所有样本点一定要在直径小于T的一个超球体内。\n",
" \n",
" 有时还会定义叶节点的分支因子L，表示每个叶节点对应的子簇的最大样本个数。\n",
" \n",
" 对于上图中的CF Tree，限定了B=7， L=5， 也就是说内部节点最多有7个子节点，而叶子节点对应的簇最多有5个样本。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 3. 聚类特征树CF Tree的生成\n",
"\n",
"\n",
"> （注意区分：样本点、CF节点（树中的才分为节点））\n",
"\n",
"　　　　下面我们看看怎么生成CF Tree。\n",
" \n",
" 我们先定义好CF Tree的参数： 即内部节点的最大子节点数B， 叶子节点对应的簇的最大样本数L， 叶节点对应的簇的最大样本直径阈值T。\n",
"\n",
"　　　　在最开始的时候，CF Tree是空的，没有任何样本，我们从训练集读入第一个样本点x1，将它放入一个新的节点A，这个节点的CF值中N=1，将这个新的节点作为根节点，此时的CF Tree如下图：\n",
"\n",
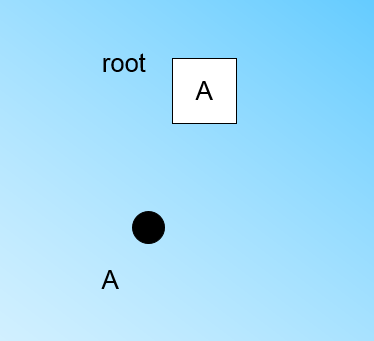"![这里写图片描述](https://img-blog.csdnimg.cn/img_convert/cd4118564af8f2fd5f8d78868911e5a8.png)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
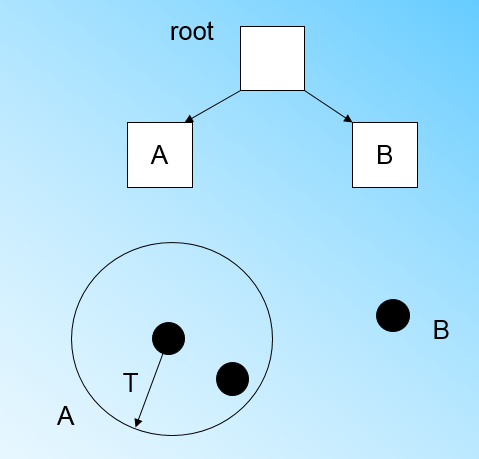
"现在我们继续读入第二个样本点x2，我们发现这个样本点和第一个样本点x1，在直径为T的超球体范围内，也就是说，他们属于一个簇，我们将第二个点也加入节点A所代表的簇中，此时需要更新节点A的CF值。\n",
"\n",
"此时A的CF值中N=2。此时的CF Tree如下图：\n",
"\n",
"![这里写图片描述](https://img-blog.csdnimg.cn/img_convert/21c12b68361d4b687669f9e84209c93f.png)\n",
"\n",
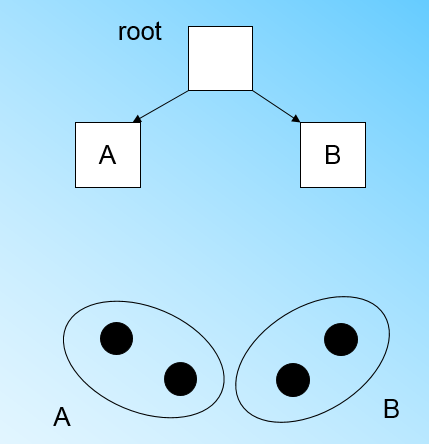
"　　　　此时来了第三个节点x3，结果我们发现这个节点不能融入刚才前面的节点形成的超球体内，也就是说，我们需要新建一个簇来容纳x3，同时为这个簇在CF树中添加一个新的节点B。\n",
" \n",
" 此时根节点有两个子节点，A和B，此时的CF Tree如下图：\n",
"\n",
"![这里写图片描述](https://img-blog.csdnimg.cn/img_convert/4ca094aa4e88394c92b8c5c3535e83dc.png)\n",
"\n",
"　　　　当来到第四个样本点x4的时候，我们发现和节点B代表的簇在直径小于T的超球体，这样更新后的CF Tree如下图：\n",
"\n",
"![这里写图片描述](https://img-blog.csdnimg.cn/img_convert/2048f92338f3ab2c167cafd87fdbc273.png)\n",
"\n",
"　　　　那个什么时候CF Tree的节点需要分裂呢？假设我们现在的CF Tree 如下图， 叶子节点LN1代表的簇有三个样本， LN2和LN3各有两个样本。我们的叶子节点的最大样本数L=3。此时一个新的样本点来了，我们发现它离LN1节点代表的簇最近，因此开始判断它是否在sc1,sc2,sc3这3个样本对应的超球体之内，但是很不幸，它不在，因此它需要建立一个新的叶子节点来容纳它。问题是我们的L=3，也就是说LN1的样本个数已经达到最大值了，不能再添加新的样本了，怎么办？此时就要将LN1叶子节点一分为二了。\n",
"\n",
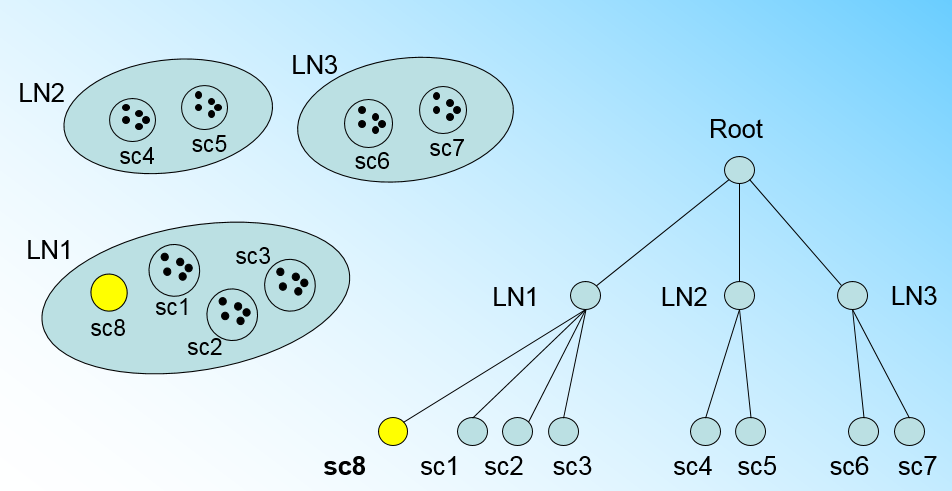"![这里写图片描述](https://img-blog.csdnimg.cn/img_convert/a713b50bc6a77e54a7e432e779f81515.png)\n",
"\n",
"　　　　我们将LN1里所有样本中，找到两个最远的样本做这两个新叶子节点的种子样本，然后将LN1节点里所有样本sc1, sc2, sc3，以及新样本点sc8划分到两个新的叶子节点上。将LN1节点划分后的CF Tree如下图：\n",
"\n",
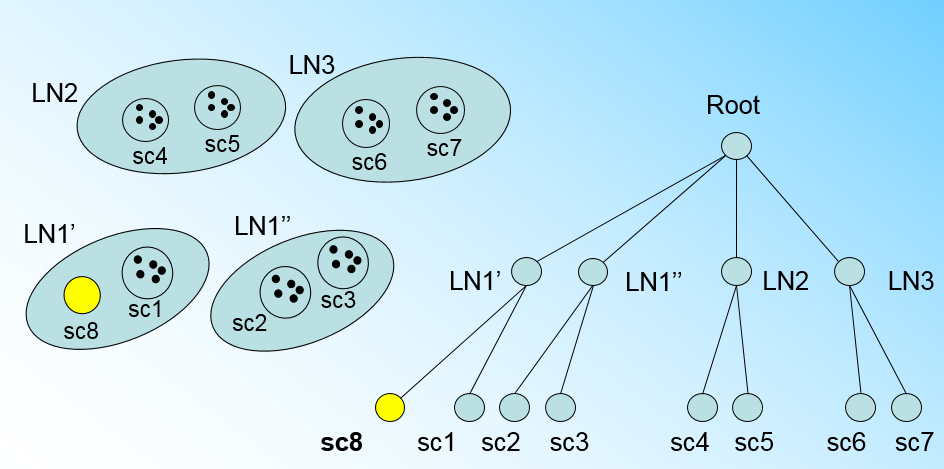"![这里写图片描述](https://img-blog.csdnimg.cn/img_convert/93ab02a692b6fcd2a785f92b35ae92e1.png)\n",
"\n",
"　　　　如果我们的内部节点的最大子节点数B=3，则此时叶子节点一分为二会导致根节点的最大子节点数超了，也就是说，我们的根节点现在也要分裂，分裂的方法和叶子节点分裂一样，分裂后的CF Tree如下图：\n",
"\n",
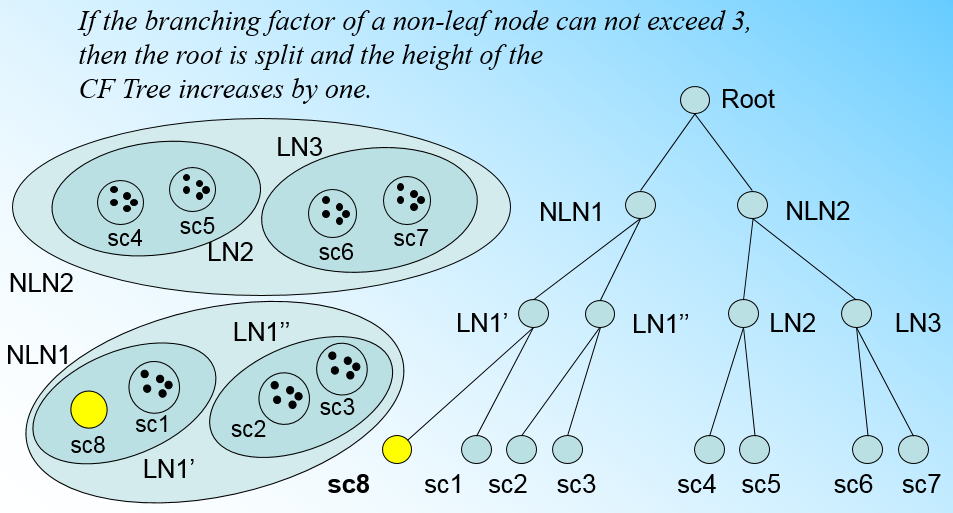"![这里写图片描述](https://img-blog.csdnimg.cn/img_convert/4e514093d36196d8e1ffa27ef7e7b7ad.png)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"有了上面这一系列的图，相信大家对于CF Tree的插入就没有什么问题了，总结下CF Tree的插入：\n",
"\n",
"　　　　1. 从根节点向下寻找和新样本距离最近的叶子节点和叶子节点里最近的样本节点\n",
"\n",
"　　　　2. 如果新样本加入后，这个样本节点对应的超球体直径仍然满足小于阈值T，则将新样本点加入叶子节点对应的簇中，并更新路径上所有的树节点，插入结束。否则转入3.\n",
" 　　　　\n",
"　　　　"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"　　　　3.将当前叶子节点划分为两个新叶子节点，选择旧叶子节点中所有样本点中距离最远的样本点，分布作为两个新叶子节点的第一个样本节点。将其他样本和新样本按照距离远近原则放入对应的叶子节点。依次向上检查父节点是否也要分裂，如果需要，按和叶子节点分裂方式相同。\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 4. BIRCH算法\n",
"\n",
"\n",
"　　　　上面讲了半天的CF Tree，终于我们可以步入正题BIRCH算法，其实将所有的训练集样本建立了CF Tree，一个基本的BIRCH算法就完成了，对应的输出就是若干树节点，每个节点里的样本点就是一个聚类的簇。也就是说BIRCH算法的主要过程，就是建立CF Tree的过程。\n",
"\n",
"　　　　当然，真实的BIRCH算法除了建立CF Tree来聚类，其实还有一些可选的算法步骤的，现在我们就来看看 BIRCH算法的流程。\n",
"\n",
"　　　　1） 将所有的样本依次读入，在内存中建立一颗CF Tree, 建立的方法参考上一节。\n",
"\n",
"　　　　2）（可选）将第一步建立的CF Tree进行筛选，去除一些异常CF节点，这些节点一般里面的样本点很少。对于一些超球体距离非常近的元组进行合并\n",
"\n",
"　　　　3）（可选）利用其它的一些聚类算法比如K-Means对所有的CF元组进行聚类，得到一颗比较好的CF Tree.这一步的主要目的是消除由于样本读入顺序导致的不合理的树结构，以及一些由于节点CF个数限制导致的树结构分裂。\n",
"\n",
"　　　　4）（可选）利用第三步生成的CF Tree的所有CF节点的质心，作为初始质心点，对所有的样本点按距离远近进行聚类。这样进一步减少了由于CF Tree的一些限制导致的聚类不合理的情况。\n",
"\n",
"　　　　从上面可以看出，BIRCH算法的关键就是步骤1，也就是CF Tree的生成，其他步骤都是为了优化最后的聚类结果。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 5. BIRCH算法小结\n",
"\n",
"\n",
"　　　　BIRCH算法可以不用输入类别数K值，这点和K-Means，Mini Batch K-Means不同。如果不输入K值，则最后的CF元组的组数即为最终的K，否则会按照输入的K值对CF元组按距离大小进行合并。\n",
"\n",
"　　　　一般来说，BIRCH算法适用于样本量较大的情况，这点和Mini Batch K-Means类似，但是BIRCH适用于类别数比较大的情况，而Mini Batch K-Means一般用于类别数适中或者较少的时候。\n",
" \n",
" BIRCH除了聚类还可以额外做一些异常点检测和数据初步按类别规约的预处理。\n",
" \n",
" 但是如果数据特征的维度非常大，比如大于20，则BIRCH不太适合，此时Mini Batch K-Means的表现较好。\n",
"\n",
"　　　　对于调参，BIRCH要比K-Means，Mini Batch K-Means复杂，因为它需要对CF Tree的几个关键的参数进行调参，这几个参数对CF Tree的最终形式影响很大。\n",
"\n",
"　　　　最后总结下BIRCH算法的优缺点：\n",
"\n",
" 　　　　BIRCH算法的主要优点有：\n",
"\n",
"　　　　1) 节约内存，所有的样本都在磁盘上，CF Tree仅仅存了CF节点和对应的指针。\n",
"\n",
"　　　　2) 聚类速度快，只需要一遍扫描训练集就可以建立CF Tree，CF Tree的增删改都很快。\n",
"\n",
"　　　　3) 可以识别噪音点，还可以对数据集进行初步分类的预处理\n",
"\n",
"　　　　BIRCH算法的主要缺点有：\n",
"\n",
"　　　　1) 由于CF Tree对每个节点的CF个数有限制，导致聚类的结果可能和真实的类别分布不同.\n",
"\n",
"　　　　2) 对高维特征的数据聚类效果不好。此时可以选择Mini Batch K-Means\n",
"\n",
"　　　　3) 如果数据集的分布簇不是类似于超球体，或者说不是凸的，则聚类效果不好。\n"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.9"
}
},
"nbformat": 4,
"nbformat_minor": 4
}

344
aihub/machine-learning/DBSCAN密度聚类.ipynb Normal file
View File

File diff suppressed because one or more lines are too long

187
aihub/machine-learning/FM-1.ipynb Normal file
View File

@ -0,0 +1,187 @@
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# FM问题来源\n",
"\n",
"\n",
"CTR/CVR预测时，用户的性别、职业、教育水平、品类偏好，商品的品类等，经过One-Hot编码转换后都会导致样本数据的稀疏性。\n",
"\n",
"特别是商品品类这种类型的特征，如商品的末级品类约有550个，采用One-Hot编码生成550个数值特征，但每个样本的这550个特征，有且仅有一个是有效的（非零）。\n",
"\n",
"由此可见，数据稀疏性是实际问题中不可避免的挑战。\n",
"\n",
"One-Hot编码的另一个特点就是导致特征空间大。\n",
"\n",
"例如，商品品类有550维特征，一个categorical特征转换为550维数值特征，特征空间剧增。\n",
"\n",
"同时通过观察大量的样本数据可以发现，某些特征经过关联之后，与label之间的相关性就会提高。例如，“USA”与“Thanksgiving”、“China”与“Chinese New Year”这样的关联特征，对用户的点击有着正向的影响。\n",
"\n",
"换句话说，来自“China”的用户很可能会在“Chinese New Year”有大量的浏览、购买行为，而在“Thanksgiving”却不会有特别的消费行为。\n",
"\n",
"这种关联特征与label的正向相关性在实际问题中是普遍存在的，如“化妆品”类商品与“女”性，“球类运动配件”的商品与“男”性，“电影票”的商品与“电影”品类偏好等。\n",
"\n",
"因此，引入两个特征的组合是非常有意义的。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# FM基本原理\n",
"\n",
"\n",
"多项式模型是包含特征组合的最直观的模型。\n",
"\n",
"在多项式模型中，特征 $x_i$ 和 $x_j$ 的组合采用 $x_ix_j$表示，即 $x_i$ 和 $x_j$ 都非零时，组合特征 $x_ix_j$ 才有意义。\n",
"\n",
"从对比的角度，本文只讨论二阶多项式模型。模型的表达式如下\n",
"\n",
"$$y(x) = w_0+ \\sum_{i=1}^n w_i x_i + \\sum_{i=1}^n \\sum_{j=i+1}^n w_{ij} x_i x_j \\tag{1}$$\n",
"\n",
"其中，$n$ 代表样本的特征数量，$x_i$ 是第 $i$ 个特征的值，$w_0$、$w_i$、$w_{ij}$是模型参数。\n",
"\n",
"从公式(1)可以看出，组合特征的参数一共有 $\\frac{n(n−1)}{2}$个，任意两个参数都是独立的。\n",
"\n",
"然而，在数据稀疏性普遍存在的实际应用场景中，二次项参数的训练是很困难的。\n",
"\n",
"其原因是，每个参数 $w_{ij}$的训练需要大量 $x_i$ 和 $x_j$ 都非零的样本；\n",
"\n",
"由于样本数据本来就比较稀疏，满足“$x_i$ 和 $x_j$ 都非零”的样本将会非常少。\n",
"\n",
"训练样本的不足，很容易导致参数 $w_{ij}$ 不准确，最终将严重影响模型的性能。\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 系数矩阵分解\n",
"\n",
"\n",
"那么，如何解决二次项参数的训练问题呢？矩阵分解提供了一种解决思路。\n",
"\n",
"与在model-based的协同过滤中，一个rating矩阵可以分解为user矩阵和item矩阵。\n",
"\n",
"对于对称矩阵W，\n",
"$$W=\n",
" \\begin{pmatrix}\n",
" \\omega_{11} & \\omega_{12}& ... &\\omega_{1n} \\\\\n",
" \\omega_{21} & \\omega_{22}& ... &\\omega_{2n} \\\\\n",
" \\vdots &\\vdots &\\ddots &\\vdots\\\\\n",
" \\omega_{n1} & \\omega_{n2}& ... &\\omega_{nn} \\\\\n",
" \\end{pmatrix}_{n\\times n}$$\n",
"\n",
"由于直接求解W不方便，因此我们引入隐变量V： \n",
"$$V=\n",
" \\begin{pmatrix}\n",
" v_{11} & v_{12}& ... &v_{1k} \\\\\n",
" v_{21} & v_{22}& ... &v_{2k} \\\\\n",
" \\vdots &\\vdots &\\ddots &\\vdots\\\\\n",
" v_{n1} & v_{n2}& ... &v_{nk} \\\\\n",
" \\end{pmatrix}_{n\\times k}=\\begin{pmatrix} \n",
"V_1^T\\\\\n",
"V_2^T\\\\\n",
"\\cdots \\\\\n",
"V_n^T\\\\\n",
"\\end{pmatrix}$$\n",
"\n",
"满足\n",
"$$VV^T = W$$\n",
"\n",
"$V$ 的第$ j$列$v_j$便是第$ j $维特征的**隐向量**。换句话说，每个参数 $w_{ij}=⟨v_i,v_j⟩$，这就是FM模型的核心思想。因此，FM的模型方程为（本文不讨论FM的高阶形式）\n",
"\n",
"$$y(x) = w_0+ \\sum_{i=1}^n w_i x_i + \\sum_{i=1}^n \\sum_{j=i+1}^n<v_i, v_j >x_i x_j \\tag{2}$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 参数个数\n",
"\n",
"\n",
"$ v_i $是第 $ i $ 维特征的隐向量，$ <·,·> $ 代表向量点积。\n",
"\n",
"隐向量的长度为 $ k （ k << n $），包含 $ k $ 个描述特征的因子。\n",
"\n",
"根据公式2，二次项的参数数量减少为 $ kn $个，远少于多项式模型的参数数量。\n",
"\n",
"另外，参数因子化使得 $ x_h x_i $ 的参数和 $ x_i x_j $ 的参数不再是相互独立的，因此我们可以在样本稀疏的情况下相对合理地估计FM的二次项参数。\n",
"\n",
"具体来说，$ x_h x_i $ 和 $ x_i x_j $ 的系数分别为 $ <v_h,v_i> $ 和 $ <v_i, v_j>$，它们之间有共同项 $ v_i $。\n",
"\n",
"也就是说，所有包含“$ x_i $ 的非零组合特征”（存在某个 $ j\\neq i $，使得 $ x_i x_j \\neq 0 $）的样本都可以用来学习隐向量 $ v_i $，这很大程度上避免了数据稀疏性造成的影响。\n",
"\n",
"而在多项式模型中，$ w_{hi} $ 和 $ w_{ij} $ 是相互独立的。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 预测时间复杂度\n",
"\n",
"显而易见，公式(2)是一个通用的拟合方程，可以采用不同的损失函数用于解决回归、二元分类等问题，比如可以采用MSE（Mean Square Error）损失函数来求解回归问题，也可以采用Hinge/Cross-Entropy损失来求解分类问题。\n",
"\n",
"当然，在进行二元分类时，FM的输出需要经过sigmoid变换，这与Logistic回归是一样的。\n",
"\n",
"当我们已经求出所有参数以后，对新输入对象进行预测时，FM的计算复杂度是 $O(kn^2)$。\n",
"\n",
"但是，通过公式(3)的等式，FM的二次项可以化简，其复杂度可以优化到 $O(kn)$。\n",
"\n",
"由此可见，**FM可以在线性时间对新样本作出预测**。\n",
"\n",
"$$\\sum_{i=1}^n \\sum_{j=i+1}^n \\langle \\mathbf{v}_i, \\mathbf{v}_j \\rangle x_i x_j = \\frac{1}{2} \\sum_{f=1}^k \\left(\\left( \\sum_{i=1}^n v_{i, f} x_i \\right)^2 - \\sum_{i=1}^n v_{i, f}^2 x_i^2 \\right) \\tag{3}$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 梯度下降法\n",
"\n",
"\n",
"利用SGD（Stochastic Gradient Descent）训练模型。模型各个参数的梯度如下\n",
"\n",
"$$\\frac{\\partial}{\\partial\\theta} y (\\mathbf{x}) = \\left\\{\\begin{array}{ll} 1, & \\text{if}\\; \\theta\\; \\text{is}\\; w_0 \\\\ x_i, & \\text{if}\\; \\theta\\; \\text{is}\\; w_i \\\\ x_i \\sum_{j=1}^n v_{j, f} x_j - v_{i, f} x_i^2, & \\text{if}\\; \\theta\\; \\text{is}\\; v_{i, f} \\end{array}\\right.$$\n",
"\n",
"\n",
"其中，$ v_{j, f} $ 是隐向量 $ v_j $ 的第 $ f $ 个元素。\n",
"\n",
"由于 $ \\sum_{j=1}^n v_{j, f} x_j $ 只与 $ f $ 有关，而与 $ i $ 无关，在每次迭代过程中，只需计算一次所有 $ f $ 的 $ \\sum_{j=1}^n v_{j, f} x_j $，就能够方便地得到所有 $ v_{i, f} $ 的梯度。\n",
"\n",
"显然，计算所有 $ f $ 的 $ \\sum_{j=1}^n v_{j, f} x_j $ 的复杂度是 $ O(kn) $；\n",
"\n",
"已知 $ \\sum_{j=1}^n v_{j, f} x_j $ 时，计算每个参数梯度的复杂度是 $ O(1) $；\n",
"\n",
"得到梯度后，更新每个参数的复杂度是 $ O(1) $；模型参数一共有 $ nk + n + 1 $ 个。\n",
"\n",
"因此，FM参数训练的复杂度也是 $ O(kn) $。综上可知，FM可以在线性时间训练和预测，是一种非常高效的模型。\n"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.9"
}
},
"nbformat": 4,
"nbformat_minor": 4
}

237
aihub/machine-learning/FM-2.ipynb Normal file
View File

File diff suppressed because one or more lines are too long

284
aihub/machine-learning/GBDT算法、XGBOOST算法-1.ipynb Normal file
View File

@ -0,0 +1,284 @@
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 1. GBDT概述\n",
"\n",
"\n",
"　　　　GBDT也是集成学习Boosting家族的成员，但是却和传统的Adaboost有很大的不同。回顾下Adaboost，我们是利用前一轮迭代弱学习器的误差率来更新训练集的权重，这样一轮轮的迭代下去。GBDT也是迭代，使用了前向分布算法，但是弱学习器限定了只能使用CART回归树模型，同时迭代思路和Adaboost也有所不同。\n",
"\n",
"　　　　在GBDT的迭代中，假设我们前一轮迭代得到的强学习器是$f_{t−1}(x)$, 损失函数是$L(y,f_{t−1}(x))$, 我们本轮迭代的目标是找到一个CART回归树模型的弱学习器$h_t(x)$，让本轮的损失损失$L(y,f_t(x))=L(y,f_{t−1}(x)+h_t(x))$最小。也就是说，本轮迭代找到决策树，要让样本的损失尽量变得更小。\n",
"\n",
"　　　　GBDT的思想可以用一个通俗的例子解释，假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。\n",
"\n",
"　　　　从上面的例子看这个思想还是蛮简单的，但是有个问题是这个损失的拟合不好度量，损失函数各种各样，怎么找到一种通用的拟合方法呢？\n",
" \n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 2. GBDT的负梯度拟合\n",
"\n",
"\n",
"在上一节中，我们介绍了GBDT的基本思路，但是没有解决损失函数拟合方法的问题。\n",
"\n",
"针对这个问题，大牛Freidman提出了用损失函数的负梯度来拟合本轮损失的近似值，进而拟合一个CART回归树。\n",
"\n",
"第$t$轮的第$i$个样本的损失函数的负梯度表示为\n",
"\n",
"$$r_{ti}=−[ \\frac {∂L(y_i,f(x_i)))}{∂f(x_i)}]_{f(x)=f_{t−1}(x)}$$\n",
"\n",
"利用$(x_i,r_{ti})(i=1,2,..m)$,我们可以拟合一颗CART回归树，得到了第$t$颗回归树，其对应的叶节点区域$R_{tj},j=1,2,...,J$。其中$J$为叶子节点的个数。\n",
"\n",
"针对每一个叶子节点里的样本，我们求出使损失函数最小，也就是拟合叶子节点最好的的输出值$c_{tj}$如下：\n",
"$$c_{tj}=\\underbrace{ arg min}_{\\rm c} \\sum_{x_i∈R_{tj}} L(y_i,f_{t−1}(x_i)+c)$$\n",
"\n",
"这样我们就得到了本轮的决策树拟合函数如下：\n",
"$$h_t(x)=\\sum_{j=1}^Jc_{tj}I(x∈R_{tj})$$\n",
"\n",
"从而本轮最终得到的强学习器的表达式如下：\n",
"$$f_t(x)=f_{t−1}(x)+\\sum_{j=1}^Jc_{tj}I(x∈R_{tj})$$\n",
"　　　　\n",
"通过损失函数的负梯度来拟合，我们找到了一种通用的拟合损失误差的办法，这样无轮是分类问题还是回归问题，我们通过其损失函数的负梯度的拟合，就可以用GBDT来解决我们的分类回归问题。区别仅仅在于损失函数不同导致的负梯度不同而已。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 3. GBDT回归算法\n",
"\n",
"\n",
"好了，有了上面的思路，下面我们总结下GBDT的回归算法。为什么没有加上分类算法一起？那是因为分类算法的输出是不连续的类别值，需要一些处理才能使用负梯度，我们后面讲。\n",
"\n",
"输入是训练集样本$T={(x_1,y_1),(x_2,y_2),...(x_m,y_m)}$， 最大迭代次数T, 损失函数L。\n",
"\n",
"输出是强学习器$f(x)$\n",
"\n",
"1) 初始化弱学习器\n",
"$$f_0(x)=\\underbrace{ arg min}_{\\rm c} \\sum_{i=1}^m L(y_i,c)$$\n",
"\n",
"2) 对迭代轮数$t=1,2,...T$有：\n",
"\n",
"　　a)对样本$i=1,2，...m$，计算负梯度\n",
"$$r_{ti}=−[ \\frac {∂L(y_i,f(x_i)))}{∂f(x_i)}]_{f(x)=f_{t−1}(x)}$$\n",
"　　b)利用$(x_i,r_{ti})(i=1,2,..m)$, 拟合一颗CART回归树,得到第t颗回归树，其对应的叶子节点区域为$R_{tj},j=1,2,...,J$。其中$J$为回归树t的叶子节点的个数。\n",
"\n",
"　　c) 对叶子区域$j =1,2,..J$,计算最佳拟合值\n",
"$$c_{tj}=\\underbrace{ arg min}_{\\rm c} \\sum_{x_i∈R_{tj}} L(y_i,f_{t−1}(x_i)+c)$$\n",
"　　　　　　\n",
"　　d) 更新强学习器\n",
"$$f_t(x)=f_{t−1}(x)+\\sum_{j=1}^Jc_{tj}I(x∈R_{tj})$$\n",
"\n",
"3) 得到强学习器f(x)的表达式\n",
"$$f(x)=f_T(x)=f_0(x)+\\sum_{t=1}^T\\sum_{j=1}^Jc_{tj}I(x∈R_{tj})$$\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 4. GBDT分类算法\n",
"\n",
"\n",
"这里我们再看看GBDT分类算法，GBDT的分类算法从思想上和GBDT的回归算法没有区别，但是由于样本输出不是连续的值，而是离散的类别，导致我们无法直接从输出类别去拟合类别输出的误差。\n",
"\n",
"为了解决这个问题，主要有两个方法，一个是用指数损失函数，此时GBDT退化为Adaboost算法。\n",
"\n",
"另一种方法是用类似于逻辑回归的对数似然损失函数的方法。\n",
"\n",
"也就是说，我们用的是类别的预测概率值和真实概率值的差来拟合损失。\n",
"\n",
"本文仅讨论用对数似然损失函数的GBDT分类。而对于对数似然损失函数，我们又有二元分类和多元分类的区别。\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 4.1 二元GBDT分类算法\n",
"\n",
"\n",
"对于二元GBDT，如果用类似于逻辑回归的对数似然损失函数，则损失函数为：\n",
"$$L(y,f(x))=log(1+exp(−yf(x)))$$\n",
"\n",
"其中$y∈\\{−1,+1\\}$。则此时的负梯度误差为\n",
"$$r_{ti}=−[\\frac {∂L(y,f(x_i)))}{∂f(x_i)}]_{f(x)=f_{t−1}(x)}=y_i/(1+exp(y_if(x_i)))$$\n",
"\n",
"对于生成的决策树，我们各个叶子节点的最佳残差拟合值为\n",
"$$c_{tj}=\\underbrace{ arg min}_{\\rm c} \\sum_{x_i∈R_{tj}} log(1+exp(−y_i(f_{t−1}(x_i)+c)))$$\n",
"　　　　　\n",
"由于上式比较难优化，我们一般使用近似值代替\n",
"$$c_{tj}=\\sum_{x_i∈R_{tj}} r_{ti}/\\sum_{x_i∈R_{tj}} |r_{ti}|(1−|r_{ti}|)$$\n",
"\n",
"除了负梯度计算和叶子节点的最佳残差拟合的线性搜索，二元GBDT分类和GBDT回归算法过程相同。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 4.2 多元GBDT分类算法\n",
"\n",
"\n",
"多元GBDT要比二元GBDT复杂一些，对应的是多元逻辑回归和二元逻辑回归的复杂度差别。假设类别数为K，则此时我们的对数似然损失函数为：\n",
"$$L(y,f(x))=−\\sum_{k=1}^Ky_k \\log p_k(x)$$\n",
"\n",
"其中如果样本输出类别为$k$，则$y_k=1$。第$k$类的概率$p_k(x)$的表达式为：\n",
"$$p_k(x)=exp(f_k(x))/\\sum_{l=1}^K exp(f_l(x))$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**通过上式我们可以看出，我们是将类别进行one-hot编码，每个输出都要建一颗决策树，一个样本通过K个决策树，得到K个输出，在通过softmax函数，获得K个概率。**\n",
"\n",
"集合上两式，我们可以计算出第$t$轮的第$i$个样本对应类别$l$的负梯度误差为\n",
"$$r_{til}=−[\\frac {∂L(y_i,f(x_i)))}{∂f(x_i)}]_{f_k(x)=f_{l,t−1}(x)}=y_{il}−p_{l,t−1}(x_i)$$\n",
"\n",
"观察上式可以看出，其实这里的误差就是样本$i$对应类别$l$的真实概率和$t−1$轮预测概率的差值。\n",
"\n",
"对于生成的决策树，我们各个叶子节点的最佳残差拟合值为\n",
"$$c_{tjl}=\\underbrace{ arg min}_{\\rm c_{jl}} \\sum_{i=0}^{m} \\sum_{k=1} ^K L(y_k,f_{t−1,l}(x)+\\sum_{j=0}^Jc_{jl}I(x_i∈R_{tj}))$$\n",
"\n",
"由于上式比较难优化，我们一般使用近似值代替\n",
"$$c_{tjl}=\\frac{K−1}{K} \\frac{\\sum_{x_i∈R_{tjl}}r_{til}}{∑_{x_i∈R_{til}}|r_{til}|(1−|r_{til}|)}$$\n",
"\n",
"除了负梯度计算和叶子节点的最佳残差拟合的线性搜索，多元GBDT分类和二元GBDT分类以及GBDT回归算法过程相同。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 5. GBDT常用损失函数\n",
"\n",
"\n",
"这里我们再对常用的GBDT损失函数做一个总结。\n",
"\n",
"**对于分类算法**，其损失函数一般有对数损失函数和指数损失函数两种:\n",
"\n",
"a) 如果是指数损失函数，则损失函数表达式为\n",
"$$L(y,f(x))=exp(−yf(x))$$\n",
"\n",
"其负梯度计算和叶子节点的最佳残差拟合参见Adaboost原理篇。\n",
"\n",
"b) 如果是对数损失函数，也就是前面说的二元分类和多元分类两种。\n",
"　　　　\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**对于回归算法**，常用损失函数有如下4种:\n",
"\n",
"　　a)均方差，这个是最常见的回归损失函数了\n",
"$$L(y,f(x))=(y−f(x))^2$$\n",
"\n",
"　　b)绝对损失，这个损失函数也很常见\n",
"$$L(y,f(x))=|y−f(x)|$$\n",
"\n",
"　　对应负梯度误差为：\n",
"$$sign(y_i−f(x_i))$$\n",
"\n",
"　　c)Huber损失，它是均方差和绝对损失的折衷产物，对于远离中心的异常点，采用绝对损失，而中心附近的点采用均方差。这个界限一般用分位数点度量。\n",
" \n",
" 损失函数如下：\n",
"$$L(y,f(x))= \\begin{cases} 0.5(y−f(x))^2, & {|y−f(x)|≤δ} \\\\ δ(|y−f(x)|−0.5δ), & {|y−f(x)|>δ} \\end{cases} $$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"对应的负梯度误差为：\n",
"　　　　\n",
"$$r(y_i,f(x_i))= \\begin{cases} y_i−f(x_i), & {|y_i−f(x_i)|≤δ} \\\\ δsign(y_i−f(x_i)), & {|y_i−f(x_i)|>δ} \\end{cases} $$\n",
"\n",
"\n",
"　 d) 分位数损失。它对应的是分位数回归的损失函数，表达式为\n",
"$$L(y,f(x))=\\sum_{y≥f(x)} θ|y−f(x)|+\\sum_{y<f(x)}(1−θ)|y−f(x)|$$\n",
"\n",
"　　　其中θ为分位数，需要我们在回归前指定。对应的负梯度误差为：\n",
"$$r(y_i,f(x_i))= \\begin{cases} θ, & {y_i≥f(x_i)} \\\\ θ−1, & {y_i<f(x_i)} \\end{cases} $$\n",
"\n",
"对于Huber损失和分位数损失，主要用于健壮回归，也就是减少异常点对损失函数的影响。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 6. GBDT的正则化\n",
"\n",
"\n",
"　　　　和Adaboost一样，我们也需要对GBDT进行正则化，防止过拟合。GBDT的正则化主要有三种方式。\n",
"\n",
"　　　　第一种是和Adaboost类似的正则化项，即**步长(learning rate)**。定义为$ν$,对于前面的弱学习器的迭代\n",
"$$f_k(x)=f_{k−1}(x)+h_k(x)$$\n",
"\n",
"　　　　如果我们加上了正则化项，则有\n",
"$$f_k(x)=f_{k−1}(x)+νh_k(x)$$\n",
"\n",
"　　　　$ν$的取值范围为$0<ν≤1$。对于同样的训练集学习效果，较小的$ν$意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。\n",
"\n",
"　　　　第二种正则化的方式是通过**子采样比例（subsample）**。取值为(0,1]。注意这里的子采样和随机森林不一样，随机森林使用的是放回抽样，而这里是不放回抽样。如果取值为1，则全部样本都使用，等于没有使用子采样。如果取值小于1，则只有一部分样本会去做GBDT的决策树拟合。选择小于1的比例可以减少方差，即防止过拟合，但是会增加样本拟合的偏差，因此取值不能太低。推荐在[0.5, 0.8]之间。\n",
"\n",
"　　　　使用了子采样的GBDT有时也称作随机梯度提升树(Stochastic Gradient Boosting Tree, SGBT)。由于使用了子采样，程序可以通过采样分发到不同的任务去做boosting的迭代过程，最后形成新树，从而减少弱学习器难以并行学习的弱点。\n",
"\n",
" \n",
"\n",
"　　　　第三种是对于弱学习器即CART回归树进行**正则化剪枝**。在决策树原理篇里我们已经讲过，这里就不重复了。\n",
"\n",
"# 7. GBDT小结\n",
"\n",
"\n",
"　　　　GBDT终于讲完了，GDBT本身并不复杂，不过要吃透的话需要对集成学习的原理，决策树原理和各种损失函树有一定的了解。由于GBDT的卓越性能，只要是研究机器学习都应该掌握这个算法，包括背后的原理和应用调参方法。目前GBDT的算法比较好的库是xgboost。当然scikit-learn也可以。\n",
"\n",
"　　　　最后总结下GBDT的优缺点。\n",
"\n",
"　　　　GBDT主要的优点有：\n",
"\n",
"　　　　1) 可以灵活处理各种类型的数据，包括连续值和离散值。GBDT使用的是cart树模型，可以处理连续值和离散值特征。对于连续值节点划分时，按照大于小于分割点，对于离散值，按照等于不等于划分分割点。\n",
"\n",
"　　　　2) 在相对少的调参时间情况下，预测的准备率也可以比较高。这个是相对SVM来说的。\n",
"\n",
"　　　　3）使用一些健壮的损失函数，对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。\n",
"\n",
"　　　　GBDT的主要缺点有：\n",
"\n",
"　　　　1)由于弱学习器之间存在依赖关系，难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。\n",
" \n",
"　　　　2）对于稀疏矩阵，容易过拟合，比lr和fm效果要差，是因为若数据中存在假象数据（例如特征f1为1的样本，输出类别都是1），树模型没法进行过拟合处理。而lr或fm可以通过正则化，压缩w1的值。\n"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.9"
}
},
"nbformat": 4,
"nbformat_minor": 4
}

217
aihub/machine-learning/GBDT算法、XGBOOST算法-2.ipynb Normal file
View File

File diff suppressed because one or more lines are too long

521
aihub/machine-learning/LightGBM算法.ipynb Normal file
View File

@ -0,0 +1,521 @@
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"安装\n",
"--\n",
"\n",
"```\n",
"pip install lightgbm\n",
"```\n",
"\n",
"gitup网址：https://github.com/Microsoft/LightGBM\n",
"\n",
"# 中文教程\n",
"\n",
"\n",
"http://lightgbm.apachecn.org/cn/latest/index.html\n"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Looking in indexes: https://mirrors.tencent.com/pypi/simple/, https://mirrors.tencent.com/repository/pypi/tencent_pypi/simple\n",
"Collecting lightgbm\n",
" Downloading https://mirrors.tencent.com/pypi/packages/a1/00/84c572ff02b27dd828d6095158f4bda576c124c4c863be7bf14f58101e53/lightgbm-3.3.2-py3-none-manylinux1_x86_64.whl (2.0 MB)\n",
" |████████████████████████████████| 2.0 MB 592 kB/s \n",
"\u001b[?25hRequirement already satisfied: numpy in /usr/local/lib/python3.6/dist-packages (from lightgbm) (1.19.4)\n",
"Requirement already satisfied: scikit-learn!=0.22.0 in /usr/local/lib/python3.6/dist-packages (from lightgbm) (0.23.2)\n",
"Requirement already satisfied: wheel in /usr/local/lib/python3.6/dist-packages (from lightgbm) (0.36.2)\n",
"Requirement already satisfied: scipy in /usr/local/lib/python3.6/dist-packages (from lightgbm) (1.5.4)\n",
"Requirement already satisfied: threadpoolctl>=2.0.0 in /usr/local/lib/python3.6/dist-packages (from scikit-learn!=0.22.0->lightgbm) (2.1.0)\n",
"Requirement already satisfied: joblib>=0.11 in /usr/local/lib/python3.6/dist-packages (from scikit-learn!=0.22.0->lightgbm) (1.0.0)\n",
"Installing collected packages: lightgbm\n",
"Successfully installed lightgbm-3.3.2\n",
"\u001b[33mWARNING: Running pip as the 'root' user can result in broken permissions and conflicting behaviour with the system package manager. It is recommended to use a virtual environment instead: https://pip.pypa.io/warnings/venv\u001b[0m\n",
"Note: you may need to restart the kernel to use updated packages.\n"
]
}
],
"source": [
"pip install lightgbm"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# lightGBM简介\n",
"\n",
"\n",
"xgboost的出现，让数据民工们告别了传统的机器学习算法们：RF、GBM、SVM、LASSO……..。\n",
"\n",
"现在微软推出了一个新的boosting框架，想要挑战xgboost的江湖地位。\n",
"\n",
"顾名思义，lightGBM包含两个关键点：light即轻量级，GBM 梯度提升机。\n",
"\n",
"LightGBM 是一个梯度 boosting 框架，使用基于学习算法的决策树。它可以说是分布式的，高效的，有以下优势：\n",
"\n",
" - 更快的训练效率\n",
"\n",
" - 低内存使用\n",
"\n",
" - 更高的准确率\n",
"\n",
" - 支持并行化学习\n",
"\n",
" - 可处理大规模数据\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# xgboost缺点\n",
"\n",
"\n",
"其缺点，或者说不足之处：\n",
"\n",
"每轮迭代时，都需要遍历整个训练数据多次。如果把整个训练数据装进内存则会限制训练数据的大小；\n",
"\n",
"如果不装进内存，反复地读写训练数据又会消耗非常大的时间。\n",
"\n",
"预排序方法（pre-sorted）：\n",
"\n",
"首先，空间消耗大。这样的算法需要保存数据的特征值，还保存了特征排序的结果（例如排序后的索引，为了后续快速的计算分割点），这里需要消耗训练数据两倍的内存。\n",
"\n",
"其次时间上也有较大的开销，在遍历每一个分割点的时候，都需要进行分裂增益的计算，消耗的代价大。\n",
"\n",
"对cache优化不友好。在预排序后，特征对梯度的访问是一种随机访问，并且不同的特征访问的顺序不一样，无法对cache进行优化。\n",
"\n",
"同时，在每一层长树的时候，需要随机访问一个行索引到叶子索引的数组，并且不同特征访问的顺序也不一样，也会造成较大的cache miss。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# lightGBM特点\n",
"\n",
"以上与其说是xgboost的不足，倒不如说是lightGBM作者们构建新算法时着重瞄准的点。\n",
"\n",
"解决了什么问题，那么原来模型没解决就成了原模型的缺点。\n",
"\n",
"概括来说，lightGBM主要有以下特点：\n",
"\n",
" - 基于Histogram的决策树算法\n",
"\n",
" - 带深度限制的Leaf-wise的叶子生长策略\n",
"\n",
" - 直方图做差加速\n",
"\n",
" - 直接支持类别特征(Categorical Feature)\n",
"\n",
" - Cache命中率优化\n",
"\n",
" - 基于直方图的稀疏特征优化\n",
"\n",
" - 多线程优化\n",
"\n",
"前2个特点使我们尤为关注的。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Histogram算法**\n",
"\n",
"直方图算法的基本思想：先把连续的浮点特征值离散化成k个整数，同时构造一个宽度为k的直方图。\n",
"\n",
"遍历数据时，根据离散化后的值作为索引在直方图中累积统计量，当遍历一次数据后，直方图累积了需要的统计量，然后根据直方图的离散值，遍历寻找最优的分割点。\n",
"\n",
"**带深度限制的Leaf-wise的叶子生长策略**\n",
"\n",
"Level-wise过一次数据可以同时分裂同一层的叶子，容易进行多线程优化，也好控制模型复杂度，不容易过拟合。\n",
"\n",
"但实际上Level-wise是一种低效算法，因为它不加区分的对待同一层的叶子，带来了很多没必要的开销，因为实际上很多叶子的分裂增益较低，没必要进行搜索和分裂。\n",
"\n",
"Leaf-wise则是一种更为高效的策略：每次从当前所有叶子中，找到分裂增益最大的一个叶子，然后分裂，如此循环。\n",
"\n",
"因此同Level-wise相比，在分裂次数相同的情况下，Leaf-wise可以降低更多的误差，得到更好的精度。\n",
"\n",
"Leaf-wise的缺点：可能会长出比较深的决策树，产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度限制，在保证高效率的同时防止过拟合。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# xgboost和lightgbm\n",
"\n",
"\n",
"**决策树算法**\n",
"\n",
"XGBoost使用的是pre-sorted算法，能够更精确的找到数据分隔点；\n",
"\n",
" - 首先，对所有特征按数值进行预排序。\n",
" \n",
" - 其次，在每次的样本分割时，用O(# data)的代价找到每个特征的最优分割点。\n",
" \n",
" - 最后，找到最后的特征以及分割点，将数据分裂成左右两个子节点。 \n",
"\n",
"优缺点： \n",
"\n",
"这种pre-sorting算法能够准确找到分裂点，但是在空间和时间上有很大的开销。 \n",
"\n",
" - i. 由于需要对特征进行预排序并且需要保存排序后的索引值（为了后续快速的计算分裂点），因此内存需要训练数据的两倍。\n",
" \n",
" - ii. 在遍历每一个分割点的时候，都需要进行分裂增益的计算，消耗的代价大。\n",
"\n",
"\n",
"\n",
"LightGBM使用的是histogram算法，占用的内存更低，数据分隔的复杂度更低。\n",
"\n",
"其思想是将连续的浮点特征离散成k个离散值，并构造宽度为k的Histogram。\n",
"\n",
"然后遍历训练数据，统计每个离散值在直方图中的累计统计量。\n",
"\n",
"在进行特征选择时，只需要根据直方图的离散值，遍历寻找最优的分割点。\n",
"\n",
"Histogram 算法的优缺点：\n",
"\n",
" - Histogram算法并不是完美的。由于特征被离散化后，找到的并不是很精确的分割点，所以会对结果产生影响。但在实际的数据集上表明，离散化的分裂点对最终的精度影响并不大，甚至会好一些。原因在于decision tree本身就是一个弱学习器，采用Histogram算法会起到正则化的效果，有效地防止模型的过拟合。\n",
" \n",
" - 时间上的开销由原来的`O(#data * #features)`降到`O(k * #features)`。由于离散化，`#bin`远小于`#data`，因此时间上有很大的提升。\n",
" \n",
" - Histogram算法还可以进一步加速。一个叶子节点的Histogram可以直接由父节点的Histogram和兄弟节点的Histogram做差得到。\n",
" \n",
" - 一般情况下，构造Histogram需要遍历该叶子上的所有数据，通过该方法，只需要遍历Histogram的k个捅。速度提升了一倍。 "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**决策树生长策略**\n",
"\n",
"XGBoost采用的是按层生长level（depth）-wise生长策略，如Figure 1所示，能够同时分裂同一层的叶子，从而进行多线程优化，不容易过拟合；但不加区分的对待同一层的叶子，带来了很多没必要的开销。\n",
"\n",
"因为实际上很多叶子的分裂增益较低，没必要进行搜索和分裂。 \n",
"\n",
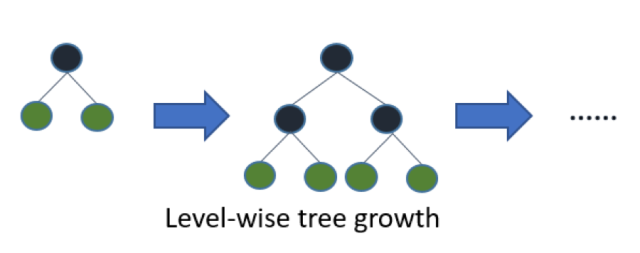"![这里写图片描述](https://imgconvert.csdnimg.cn/aHR0cDovLzViMDk4OGU1OTUyMjUuY2RuLnNvaHVjcy5jb20vaW1hZ2VzLzIwMTcxMTIzL2NlOTQ4MjhlN2I3YTQ1ODBhNTlhMGY5MWQ5NWU1ZjgzLnBuZw?x-oss-process=image/format,png)\n",
"\n",
"LightGBM采用leaf-wise生长策略，如Figure 2所示，每次从当前所有叶子中找到分裂增益最大（一般也是数据量最大）的一个叶子，然后分裂，如此循环。\n",
"\n",
"因此同Level-wise相比，在分裂次数相同的情况下，Leaf-wise可以降低更多的误差，得到更好的精度。Leaf-wise的缺点是可能会长出比较深的决策树，产生过拟合。\n",
"\n",
"因此LightGBM在Leaf-wise之上增加了一个最大深度的限制，在保证高效率的同时防止过拟合。 \n",
"\n",
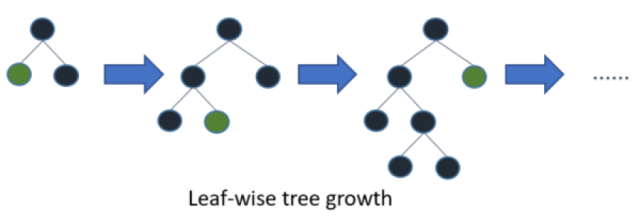"![这里写图片描述](https://imgconvert.csdnimg.cn/aHR0cDovLzViMDk4OGU1OTUyMjUuY2RuLnNvaHVjcy5jb20vaW1hZ2VzLzIwMTcxMTIzLzAxNTlhMzk5MGE1NDRkMDBhNmNkMDI1ZDlhMzNiNDk5LnBuZw?x-oss-process=image/format,png)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**网络通信优化**\n",
"\n",
"XGBoost由于采用pre-sorted算法，通信代价非常大，所以在并行的时候也是采用histogram算法；\n",
"\n",
"LightGBM采用的histogram算法通信代价小，通过使用集合通信算法，能够实现并行计算的线性加速。\n",
"\n",
"**LightGBM支持类别特征**\n",
"\n",
"实际上大多数机器学习工具都无法直接支持类别特征，一般需要把类别特征，转化one-hotting特征，降低了空间和时间的效率。\n",
"\n",
"而类别特征的使用是在实践中很常用的。基于这个考虑，LightGBM优化了对类别特征的支持，可以直接输入类别特征，不需要额外的0/1展开。\n",
"\n",
"并在决策树算法上增加了类别特征的决策规则。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# lightGBM调参\n",
"\n",
"\n",
"所有的参数含义，参考：http://lightgbm.apachecn.org/cn/latest/Parameters.html\n",
"\n",
"调参过程：\n",
"\n",
"（1）num_leaves\n",
"\n",
"LightGBM使用的是leaf-wise的算法，因此在调节树的复杂程度时，使用的是num_leaves而不是max_depth。\n",
"\n",
"大致换算关系：num_leaves = 2^(max_depth)\n",
"\n",
"（2）样本分布非平衡数据集：可以param[‘is_unbalance’]=’true’\n",
"\n",
"（3）Bagging参数：bagging_fraction+bagging_freq（必须同时设置）、feature_fraction\n",
"\n",
"（4）min_data_in_leaf、min_sum_hessian_in_leaf"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"sklearn接口形式的LightGBM示例\n",
"--\n",
"\n",
"这里主要以sklearn的使用形式来使用lightgbm算法，包含建模，训练，预测，网格参数优化。"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Load data...\n",
"Start training...\n",
"[1]\tvalid_0's l1: 0.588034\tvalid_0's l2: 0.557257\n",
"[2]\tvalid_0's l1: 0.558601\tvalid_0's l2: 0.504\n",
"[3]\tvalid_0's l1: 0.533366\tvalid_0's l2: 0.457982\n",
"[4]\tvalid_0's l1: 0.507443\tvalid_0's l2: 0.41463\n",
"[5]\tvalid_0's l1: 0.485721\tvalid_0's l2: 0.379804\n",
"[6]\tvalid_0's l1: 0.465626\tvalid_0's l2: 0.344388\n",
"[7]\tvalid_0's l1: 0.44743\tvalid_0's l2: 0.316163\n",
"[8]\tvalid_0's l1: 0.429186\tvalid_0's l2: 0.287238\n",
"[9]\tvalid_0's l1: 0.411935\tvalid_0's l2: 0.262292\n",
"[10]\tvalid_0's l1: 0.395375\tvalid_0's l2: 0.238778\n",
"[11]\tvalid_0's l1: 0.380425\tvalid_0's l2: 0.220261\n",
"[12]\tvalid_0's l1: 0.365386\tvalid_0's l2: 0.201077\n",
"[13]\tvalid_0's l1: 0.351844\tvalid_0's l2: 0.186131\n",
"[14]\tvalid_0's l1: 0.338187\tvalid_0's l2: 0.170488\n",
"[15]\tvalid_0's l1: 0.32592\tvalid_0's l2: 0.158447\n",
"[16]\tvalid_0's l1: 0.313696\tvalid_0's l2: 0.14627\n",
"[17]\tvalid_0's l1: 0.301835\tvalid_0's l2: 0.13475\n",
"[18]\tvalid_0's l1: 0.291441\tvalid_0's l2: 0.126063\n",
"[19]\tvalid_0's l1: 0.280924\tvalid_0's l2: 0.117155\n",
"[20]\tvalid_0's l1: 0.270932\tvalid_0's l2: 0.109156\n",
"Start predicting...\n",
"The rmse of prediction is: 0.33038813204779693\n",
"Feature importances: [8, 0, 41, 8]\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"/usr/local/lib/python3.6/dist-packages/lightgbm/sklearn.py:726: UserWarning: 'early_stopping_rounds' argument is deprecated and will be removed in a future release of LightGBM. Pass 'early_stopping()' callback via 'callbacks' argument instead.\n",
" _log_warning(\"'early_stopping_rounds' argument is deprecated and will be removed in a future release of LightGBM. \"\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Best parameters found by grid search are: {'learning_rate': 0.1, 'n_estimators': 40}\n"
]
}
],
"source": [
"import lightgbm as lgb\n",
"import pandas as pd\n",
"from sklearn.metrics import mean_squared_error\n",
"from sklearn.model_selection import GridSearchCV\n",
"from sklearn.datasets import load_iris\n",
"from sklearn.model_selection import train_test_split\n",
"from sklearn.datasets import make_classification\n",
"# 加载数据\n",
"print('Load data...')\n",
"\n",
"iris = load_iris()\n",
"data=iris.data\n",
"target = iris.target\n",
"X_train,X_test,y_train,y_test =train_test_split(data,target,test_size=0.2)\n",
"\n",
"# df_train = pd.read_csv('../regression/regression.train', header=None, sep='\\t')\n",
"# df_test = pd.read_csv('../regression/regression.test', header=None, sep='\\t')\n",
"# y_train = df_train[0].values\n",
"# y_test = df_test[0].values\n",
"# X_train = df_train.drop(0, axis=1).values\n",
"# X_test = df_test.drop(0, axis=1).values\n",
"\n",
"print('Start training...')\n",
"# 创建模型，训练模型\n",
"gbm = lgb.LGBMRegressor(objective='regression',num_leaves=31,learning_rate=0.05,n_estimators=20)\n",
"gbm.fit(X_train, y_train,eval_set=[(X_test, y_test)],eval_metric='l1',early_stopping_rounds=5)\n",
"\n",
"print('Start predicting...')\n",
"# 测试机预测\n",
"y_pred = gbm.predict(X_test, num_iteration=gbm.best_iteration_)\n",
"# 模型评估\n",
"print('The rmse of prediction is:', mean_squared_error(y_test, y_pred) ** 0.5)\n",
"\n",
"# feature importances\n",
"print('Feature importances:', list(gbm.feature_importances_))\n",
"\n",
"# 网格搜索，参数优化\n",
"estimator = lgb.LGBMRegressor(num_leaves=31)\n",
"\n",
"param_grid = {\n",
" 'learning_rate': [0.01, 0.1, 1],\n",
" 'n_estimators': [20, 40]\n",
"}\n",
"\n",
"gbm = GridSearchCV(estimator, param_grid)\n",
"\n",
"gbm.fit(X_train, y_train)\n",
"\n",
"print('Best parameters found by grid search are:', gbm.best_params_)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 原生形式使用lightgbm"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Start training...\n",
"[LightGBM] [Warning] Auto-choosing col-wise multi-threading, the overhead of testing was 0.000061 seconds.\n",
"You can set `force_col_wise=true` to remove the overhead.\n",
"[LightGBM] [Info] Total Bins 88\n",
"[LightGBM] [Info] Number of data points in the train set: 120, number of used features: 4\n",
"[LightGBM] [Info] Start training from score 0.983333\n",
"[LightGBM] [Warning] No further splits with positive gain, best gain: -inf\n",
"[1]\tvalid_0's auc: 0.973545\tvalid_0's l2: 0.613932\n",
"Training until validation scores don't improve for 5 rounds\n",
"[LightGBM] [Warning] No further splits with positive gain, best gain: -inf\n",
"[2]\tvalid_0's auc: 0.973545\tvalid_0's l2: 0.564205\n",
"[LightGBM] [Warning] No further splits with positive gain, best gain: -inf\n",
"[3]\tvalid_0's auc: 0.97619\tvalid_0's l2: 0.516368\n",
"[LightGBM] [Warning] No further splits with positive gain, best gain: -inf\n",
"[4]\tvalid_0's auc: 0.97619\tvalid_0's l2: 0.475329\n",
"[LightGBM] [Warning] No further splits with positive gain, best gain: -inf\n",
"[5]\tvalid_0's auc: 0.97619\tvalid_0's l2: 0.436004\n",
"[LightGBM] [Warning] No further splits with positive gain, best gain: -inf\n",
"[6]\tvalid_0's auc: 1\tvalid_0's l2: 0.40095\n",
"[LightGBM] [Warning] No further splits with positive gain, best gain: -inf\n",
"[7]\tvalid_0's auc: 1\tvalid_0's l2: 0.36919\n",
"[LightGBM] [Warning] No further splits with positive gain, best gain: -inf\n",
"[8]\tvalid_0's auc: 1\tvalid_0's l2: 0.338404\n",
"[LightGBM] [Warning] No further splits with positive gain, best gain: -inf\n",
"[9]\tvalid_0's auc: 1\tvalid_0's l2: 0.310487\n",
"[LightGBM] [Warning] No further splits with positive gain, best gain: -inf\n",
"[10]\tvalid_0's auc: 1\tvalid_0's l2: 0.285916\n",
"[LightGBM] [Warning] No further splits with positive gain, best gain: -inf\n",
"[11]\tvalid_0's auc: 1\tvalid_0's l2: 0.264549\n",
"Early stopping, best iteration is:\n",
"[6]\tvalid_0's auc: 1\tvalid_0's l2: 0.40095\n",
"Save model...\n",
"Start predicting...\n",
"The rmse of prediction is: 0.6332058050413797\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"/usr/local/lib/python3.6/dist-packages/lightgbm/engine.py:181: UserWarning: 'early_stopping_rounds' argument is deprecated and will be removed in a future release of LightGBM. Pass 'early_stopping()' callback via 'callbacks' argument instead.\n",
" _log_warning(\"'early_stopping_rounds' argument is deprecated and will be removed in a future release of LightGBM. \"\n"
]
}
],
"source": [
"# coding: utf-8\n",
"# pylint: disable = invalid-name, C0111\n",
"import json\n",
"import lightgbm as lgb\n",
"import pandas as pd\n",
"from sklearn.metrics import mean_squared_error\n",
"from sklearn.datasets import load_iris\n",
"from sklearn.model_selection import train_test_split\n",
"from sklearn.datasets import make_classification\n",
"\n",
"iris = load_iris()\n",
"data=iris.data\n",
"target = iris.target\n",
"X_train,X_test,y_train,y_test =train_test_split(data,target,test_size=0.2)\n",
"\n",
"\n",
"# 加载你的数据\n",
"# print('Load data...')\n",
"# df_train = pd.read_csv('../regression/regression.train', header=None, sep='\\t')\n",
"# df_test = pd.read_csv('../regression/regression.test', header=None, sep='\\t')\n",
"#\n",
"# y_train = df_train[0].values\n",
"# y_test = df_test[0].values\n",
"# X_train = df_train.drop(0, axis=1).values\n",
"# X_test = df_test.drop(0, axis=1).values\n",
"\n",
"# 创建成lgb特征的数据集格式\n",
"lgb_train = lgb.Dataset(X_train, y_train)\n",
"lgb_eval = lgb.Dataset(X_test, y_test, reference=lgb_train)\n",
"\n",
"# 将参数写成字典下形式\n",
"params = {\n",
" 'task': 'train',\n",
" 'boosting_type': 'gbdt', # 设置提升类型\n",
" 'objective': 'regression', # 目标函数\n",
" 'metric': {'l2', 'auc'}, # 评估函数\n",
" 'num_leaves': 31, # 叶子节点数\n",
" 'learning_rate': 0.05, # 学习速率\n",
" 'feature_fraction': 0.9, # 建树的特征选择比例\n",
" 'bagging_fraction': 0.8, # 建树的样本采样比例\n",
" 'bagging_freq': 5, # k 意味着每 k 次迭代执行bagging\n",
" 'verbose': 1 # <0 显示致命的, =0 显示错误 (警告), >0 显示信息\n",
"}\n",
"\n",
"print('Start training...')\n",
"# 训练 cv and train\n",
"gbm = lgb.train(params,lgb_train,num_boost_round=20,valid_sets=lgb_eval,early_stopping_rounds=5)\n",
"\n",
"print('Save model...')\n",
"# 保存模型到文件\n",
"gbm.save_model('model.txt')\n",
"\n",
"print('Start predicting...')\n",
"# 预测数据集\n",
"y_pred = gbm.predict(X_test, num_iteration=gbm.best_iteration)\n",
"# 评估模型\n",
"print('The rmse of prediction is:', mean_squared_error(y_test, y_pred) ** 0.5)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.9"
}
},
"nbformat": 4,
"nbformat_minor": 4
}

346
aihub/machine-learning/gbdt构建新特征.ipynb Normal file
View File

File diff suppressed because one or more lines are too long

461
aihub/machine-learning/kmean-kd.ipynb Normal file
View File

File diff suppressed because one or more lines are too long

462
aihub/machine-learning/k均值聚类、k中心点聚类.ipynb Normal file
View File

@ -0,0 +1,462 @@
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"上一篇我们学习了层次聚类。层次聚类只是迭代的把最相近的两个聚类匹配起来。\n",
"\n",
"并没有给出能给出多少的分组。\n",
"\n",
"今天我们来研究一个K均值聚类。就是给定分组数目的基础上再来聚类。即将所有的样本数据集分成K个组，每个组内尽可能相似，每个组间又尽可能不相似。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"k均值聚类和k中心点聚类属于基于划分的聚类。\n",
"\n",
"也就是给定了k值（簇的个数），我们通过不停的设计每个对象该属于哪个簇而实现聚类。\n",
"\n",
"我们今天使用k均值为文档进行分组。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# K均值聚类"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"K-means算法是很典型的基于距离的聚类算法，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。\n",
"\n",
"该算法认为簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。算法采用误差平方和准则函数作为聚类准则函数。\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"算法过程如下：\n",
"\n",
"1）从N个文档随机选取K个文档作为质心\n",
"\n",
"2）对剩余的每个文档测量其到每个质心的距离，并把它归到最近的质心的类\n",
"\n",
"3）重新计算已经得到的各个类的质心\n",
"\n",
"4）迭代2～3步直至新的质心与原质心相等或小于指定阈值，算法结束"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"具体如下：\n",
"\n",
"输入：k, data; 其中data为n个样本集\n",
"\n",
"（1） 随机选择k个初始中心点，例如c[0]=data[0],…c[k-1]=data[k-1]；\n",
"\n",
"（2） 对于data[0]….data[n]，分别与c[0]…c[k-1]比较，假定与c[i]差值最少，就标记为i；\n",
"\n",
"（3） 对于所有标记为i点，重新计算c[i]={ 所有标记为i的data[j]之和}/标记为i的个数；\n",
"\n",
"（4） 重复(2)(3)，直到所有c[i]值的变化小于给定阈值。\n",
"\n",
"![这里写图片描述](https://img-blog.csdnimg.cn/img_convert/b23dffdaec74ee623cb63667786f9b3f.png)\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 案例实现"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 加载数据集\n",
"\n",
"\n",
"使用我们一贯的文本数据集结构。每行为一个文档（链接或者文档名），每列为一个文档特征（单词），每个单元格的取值为单词在文档中出现的次数。\n",
"\n",
"[博客数据集点击下载](http://luanpeng.oss-cn-qingdao.aliyuncs.com/csdn/python/%E8%81%9A%E7%B1%BB/blogdata.txt)"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"--2022-09-20 23:56:00-- http://luanpeng.oss-cn-qingdao.aliyuncs.com/csdn/python/%E8%81%9A%E7%B1%BB/blogdata.txt\n",
"Resolving luanpeng.oss-cn-qingdao.aliyuncs.com (luanpeng.oss-cn-qingdao.aliyuncs.com)... 47.104.37.237\n",
"Connecting to luanpeng.oss-cn-qingdao.aliyuncs.com (luanpeng.oss-cn-qingdao.aliyuncs.com)|47.104.37.237|:80... connected.\n",
"HTTP request sent, awaiting response... 200 OK\n",
"Length: 147123 (144K) [text/plain]\n",
"Saving to: ‘blogdata.txt’\n",
"\n",
"blogdata.txt 100%[===================>] 143.67K --.-KB/s in 0.06s \n",
"\n",
"2022-09-20 23:56:00 (2.25 MB/s) - ‘blogdata.txt’ saved [147123/147123]\n",
"\n"
]
}
],
"source": [
"!wget http://luanpeng.oss-cn-qingdao.aliyuncs.com/csdn/python/%E8%81%9A%E7%B1%BB/blogdata.txt"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"```\n",
"Blog china kids music yahoo want ...\n",
"Wonkette 0 2 1 0 6 ...\n",
"Publishing 2 0 0 7 4 ...\n",
"... ... ... ... ... ... ...\n",
"```"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"```\n",
"\n",
"代码完成加载数据集，获取列名，行名，样本数据集\n",
"\n",
"```"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"# 读取表格型数据，获取特征数据集。\n",
"def readfile(filename):\n",
" lines=[line for line in open(filename)]\n",
"\n",
" # 第一行是列标题\n",
" colnames=lines[0].strip().split('\\t')[1:]\n",
" rownames=[]\n",
" data=[]\n",
" for line in lines[1:]:\n",
" p=line.strip().split('\\t')\n",
" # 每行的第一列是行名\n",
" rownames.append(p[0])\n",
" # 剩余部分就是该行对应的数据\n",
" onerow = [float(x) for x in p[1:]]\n",
" data.append(onerow)\n",
" return rownames,colnames,data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 距离计算\n",
"\n",
"前面的文章我们已经了解了有欧式距离和皮尔逊相似度代表两个数组的亲密度。\n",
"\n",
"欧式距离计算简单，皮尔逊相似度稍微复杂些，不过在下面几种情况时效果好。\n",
"\n",
"1、在两个数组的尺度不相同，但是变化率相同时，效果好。比如，一个数组为[7,8,9]，一个数组为[1,2,3]其实这两种具有很强的相似度，只不过在尺度表现上不同罢了。\n",
"\n",
"2、在两个数组所具有的属性数目上不同时效果好。比如，一个数组为[1,5,9]和另一个数组[1,2,3,4,5,6,7,8,9]这两个数组也是具有很好的相似度的。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"在层次聚类中我们使用皮尔逊相似度来代替节点间距离。\n",
"\n",
"这是因为每个博客所拥有的特征属性的数目差距可能是很大的。\n",
"\n",
"皮尔逊的实现代码"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"# 计算两行的皮尔逊相似度\n",
"def pearson(v1,v2):\n",
" # 简单求和\n",
" sum1=sum(v1)\n",
" sum2=sum(v2)\n",
"\n",
" # 求平方和\n",
" sum1Sq=sum([pow(v,2) for v in v1])\n",
" sum2Sq=sum([pow(v,2) for v in v2])\n",
"\n",
" # 求乘积之和\n",
" pSum=sum([v1[i]*v2[i] for i in range(len(v1))])\n",
"\n",
" # 计算r\n",
" num=pSum-(sum1*sum2/len(v1))\n",
" den=sqrt((sum1Sq-pow(sum1,2)/len(v1))*(sum2Sq-pow(sum2,2)/len(v1)))\n",
" if den==0: return 0\n",
"\n",
" return 1.0-num/den"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"注意，在我们使用的博客数据集中，每个单元格的取值是单词在博客中出现的次数。\n",
"不过在有些统计中，只关系单词是否在博客中出现，而不关系出现的次数。\n",
"\n",
"只要单词出现，则取值为1，单词不出现则取值为0。假如我们对同时希望拥有两件物品的人在物品方面互有重叠的情况进行度量。\n",
"\n",
"我们采用Tanimoto系数的度量方法，它代表的是交集与并集的比率。\n",
"\n",
"Tanimoto系数的计算实现"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"# 使用tanimoto系数表示距离（相似度）：两个向量的交集/两个向量的并集\n",
"def tanamoto(v1,v2):\n",
" c1,c2,shr=0,0,0\n",
" for i in range(len(v1)):\n",
" if v1[i]!=0: c1+=1 # 出现在v1中\n",
" if v2[i]!=0: c2+=1 # 出现在v2中\n",
" if v1[i]!=0 and v2[i]!=0: shr+=1 # 在两个向量中都出现\n",
"\n",
" return 1.0-(float(shr)/(c1+c2-shr))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 迭代实现k均值聚类\n",
"\n",
"\n",
"随机设置k个聚类点，根据每个点到k个聚类点的距离，为每个点分组。移动聚类点到组成员中心位置。重新计算重新分组重新移动。迭代至成员不再变化。\n",
"\n",
"函数 返回k个聚类点，以及所包含的所有成员\n"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [],
"source": [
"import random\n",
"# 每个点代表一行，每个聚类点，代表一类。参数：rows数据集，distance距离计算算法，k聚类的数目。\n",
"def kcluster(rows,distance=pearson,k=4):\n",
" # 确定每个点的特征的最小值和最大值\n",
" ranges=[(min([row[i] for row in rows]),max([row[i] for row in rows])) for i in range(len(rows[0]))]\n",
"\n",
" # 随机创建K个中心点\n",
" clusters=[[random.random()*(ranges[i][1]-ranges[i][0])+ranges[i][0]\n",
" for i in range(len(rows[0]))] for j in range(k)]\n",
"\n",
" lastmatches=None\n",
" for t in range(100): #默认迭代100次。\n",
" print('迭代 %d' % t)\n",
" bestmatches=[[] for i in range(k)] #生成k个空数组，用于存储k个聚类点包含的成员\n",
"\n",
" # 在每一行中寻找距离最近的中心点\n",
" for j in range(len(rows)):\n",
" row=rows[j]\n",
" bestmatch=0\n",
" for i in range(k):\n",
" d=distance(clusters[i],row)\n",
" if d<distance(clusters[bestmatch],row): bestmatch=i #计算与哪个聚类点最近\n",
" bestmatches[bestmatch].append(j) #每个聚类点记录它包含的组成员\n",
"\n",
" # 如果结果与上一次相同，则整个过程结束\n",
" if bestmatches==lastmatches: break\n",
" lastmatches=bestmatches\n",
"\n",
" # 把中心点移动到成员的平均位置处\n",
" for i in range(k):\n",
" avgs=[0.0]*len(rows[0])\n",
" if len(bestmatches[i])>0:\n",
" for rowid in bestmatches[i]:\n",
" for m in range(len(rows[rowid])):\n",
" avgs[m]+=rows[rowid][m]\n",
" for j in range(len(avgs)): #在每个维度都计算均值\n",
" avgs[j]/=len(bestmatches[i])\n",
" clusters[i]=avgs\n",
"\n",
" return bestmatches #返回k个聚类点，以及所包含的所有成员"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 测试\n",
"\n",
"\n",
"下面我们就可以来测试一下了。\n"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"迭代 0\n",
"迭代 1\n",
"迭代 2\n",
"迭代 3\n",
"迭代 4\n",
"['Mashable!', 'Slashdot', 'The Blotter', 'Schneier on Security', 'Signum sine tinnitu--by Guy Kawasaki', 'MetaFilter']\n"
]
}
],
"source": [
"if __name__=='__main__':\n",
" from math import sqrt\n",
" blognames,words,data = readfile('blogdata.txt') #加载数据集\n",
" kclust = kcluster(data,k=10) #k均值聚类，形成k个聚类\n",
" print([blognames[r] for r in kclust[0]]) # 打印第一个聚类的所有博客名称"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"输出结果\n",
"\n",
"```\n",
"迭代 0\n",
"\n",
"迭代 1\n",
"\n",
"迭代 2\n",
"\n",
"迭代 3\n",
"\n",
"迭代 4\n",
"\n",
"[\"The Superficial - Because You're Ugly\", 'Joho the Blog', 'Go Fug Yourself', \"O'Reilly Radar\", 'Topix.net Weblog', 'flagrantdisregard', 'The Blotter', 'Schneier on Security']\n",
"```"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"可以看到只迭代了5次就成功聚类完成。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# k-means聚类的优缺点：\n",
"\n",
" **k-means算法的优点：**\n",
"\n",
"（1）k-means算法是解决聚类问题的一种经典算法，算法简单、快速。\n",
"\n",
"（2）对处理大数据集，该算法是相对可伸缩的和高效率的，因为它的复杂度大约是O(nkt)，其中n是所有对象的数目，k是簇的数目,t是迭代的次数。通常`k<<n`。这个算法通常局部收敛。\n",
"\n",
"（3）算法尝试找出使平方误差函数值最小的k个划分。当簇是密集的、球状或团状的，且簇与簇之间区别明显时，聚类效果较好。\n",
"\n",
"**缺点：**\n",
"\n",
"（1）k-平均方法只有在簇的平均值被定义的情况下才能使用，且对有些分类属性的数据不适合。\n",
"\n",
"（2）要求用户必须事先给出要生成的簇的数目k。\n",
"\n",
"（3）对初值敏感，对于不同的初始值，可能会导致不同的聚类结果。\n",
"\n",
"（4）不适合于发现非凸面形状的簇，或者大小差别很大的簇。\n",
"\n",
"（5）对于\"噪声\"和孤立点数据敏感，少量的该类数据能够对平均值产生极大影响。\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# k中心点算法\n",
"\n",
"\n",
"k中心算法的基本过程是:\n",
"\n",
"首先为每个簇随意选择一个代表对象，剩余的对象根据其与每个代表对象的距离（此处距离不一定是欧氏距离，也可能是曼哈顿距离）分配给最近的代表对象所代表的簇；\n",
"\n",
"然后反复用非代表对象来代替代表对象，以优化聚类质量。\n",
"\n",
"聚类质量用一个代价函数来表示。当一个中心点被某个非中心点替代时，除了未被替换的中心点外，其余各点被重新分配。\n",
"\n",
"为了减轻k均值算法对孤立点的敏感性，k中心点算法不采用簇中对象的平均值作为簇中心，而选用簇中离平均值最近的对象作为簇中心。\n",
"\n",
"算法如下:\n",
"\n",
"输入:包含n个对象的数据库和簇数目k；\n",
"\n",
"输出:k个簇\n",
"\n",
" （1）随机选择k个代表对象作为初始的中心点\n",
"\n",
" （2）指派每个剩余对象给离它最近的中心点所代表的簇\n",
"\n",
" （3）随机地选择一个非中心点对象y\n",
"\n",
" （4）计算用y代替中心点x的总代价s\n",
"\n",
" （5）如果s为负，则用可用y代替x，形成新的中心点\n",
" \n",
" （6）重复(2)(3)(4)(5)，直到k个中心点不再发生变化."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.9"
}
},
"nbformat": 4,
"nbformat_minor": 4
}

272
aihub/machine-learning/最小生成树（MST）的Prim算法和Kruskal算法.ipynb Normal file
View File

@ -0,0 +1,272 @@
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 最小生成树MST\n",
"\n",
"\n",
"一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。\n",
"\n",
"也就是说，用原图中有的边，连接n个节点，保证每个节点都被连接，且使用的边的数目最少。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 最小权重生成树\n",
"\n",
"\n",
"在一给定的无向图$G = (V, E) $中，$(u, v) $代表连接顶点$ u $与顶点 $v $的边（即），而 $w(u, v) $代表此边的权重，若存在 $T $为$ E $的子集（即）且为无循环图，使得\n",
"\n",
"$$w(t)=\\sum_{(u,v)\\in t}w(u,v)$$\n",
"\n",
"的$ w(T) $最小，则此 $T$ 为 $G$ 的最小生成树。\n",
" \n",
"最小生成树其实是最小权重生成树的简称。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 应用：\n",
"\n",
"\n",
"例如：要在n个城市之间铺设光缆，主要目标是要使这 n 个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。\n",
"\n",
"这就需要找到带权的最小生成树"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Prim算法\n",
"\n",
"\n",
"1)、输入：一个加权连通图，其中顶点集合为$V$，边集合为$E$；\n",
"\n",
"2)、初始化：$V_{new}= \\{x\\}$，其中$x$为集合$V$中的任一节点（起始点），$E_{new}= \\{\\}$,为空；\n",
"\n",
"3)、重复下列操作，直到$V_{new}= V$：\n",
"\n",
" - a.在集合$E$中选取权值最小的边$<u, v>$，其中$u$为集合$V_{new}$中的元素，而$v$不在$V_{new}$集合当中，并且$v∈V$（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；\n",
" \n",
" - b.将$v$加入集合$V_{new}$中，将$<u, v>$边加入集合$E_{new}$中；\n",
"\n",
"4)、输出：使用集合$V_{new}$和$E_{new}$来描述所得到的最小生成树"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Kruskal算法简述\n",
"\n",
"假设 $W_N=(V,{E}) $是一个含有n 个顶点的连通网，则按照克鲁斯卡尔算法构造最小生成树的过程为：\n",
"\n",
"先构造一个只含 n 个顶点，而边集为空的子图，若将该子图中各个顶点看成是各棵树上的根结点，则它是一个含有 n 棵树的一个森林。\n",
"\n",
"之后，从网的边集 $E$ 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，也就是说，将这两个顶点分别所在的两棵树合成一棵树；\n",
"\n",
"反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。\n",
"\n",
"依次类推，直至森林中只有一棵树，也即子图中含有 n-1条边为止。\n",
"\n",
"循环中可加入已加入MST的点的数量的判断，有可能提前结束循环，提高效率。\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"下面是hdu1233的源代码，一个用Prim算法，另一个用Kruskal，标准的MST问题。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"#include <cstdio.h>\n",
"#include <algorithm>\n",
"using namespace std;\n",
"\n",
"typedef int weight_t; \n",
"\n",
"#define SIZE 101\n",
"\n",
"int N;\n",
"\n",
"//图的邻接矩阵\n",
"weight_t Graph[SIZE][SIZE];\n",
"\n",
"//各顶点到中间结果的最短距离，始终维护\n",
"weight_t D[SIZE];\n",
"\n",
"//标志位\n",
"bool Flag[SIZE];\n",
"\n",
"//Prim算法，返回MST的长度\n",
"weight_t Prim(){\n",
"\t//初始化数组\n",
"\tfill(D,D+SIZE,INT_MAX);\n",
"\tfill(Flag,Flag+SIZE,false);\n",
"\n",
"\t//初始化第一个计算的点\n",
"\tD[1] = 0;\n",
"\n",
"\tweight_t ans = 0;\n",
"\n",
"\tfor(int i=1;i<=N;++i){\n",
"\t\t//找出距离中间结果最近的点\n",
"\t\tint k = -1;\n",
"\t\tfor(int j=1;j<=N;++j)\n",
"\t\t\tif ( !Flag[j] && ( -1 == k || D[j] < D[k] ) )\n",
"\t\t\t\tk = j;\n",
"\n",
"\t\t//将k点加入中间结果\n",
"\t\tFlag[k] = true;\n",
"\t\tans += D[k];\n",
"\n",
"\t\t//更新剩余点到中间结果的最短距离\n",
"\t\tfor(int j=1;j<=N;++j)\n",
"\t\t\tif ( !Flag[j] && Graph[k][j] < D[j] )\n",
"\t\t\t\tD[j] = Graph[k][j];\n",
"\t}\n",
"\n",
"\treturn ans;\n",
"}\n",
"\n",
"bool read(){\n",
"\tscanf(\"%d\",&N);\n",
"\tif ( 0 == N ) return false;\n",
"\t\n",
"\tfor(int i=0;i<N*(N-1)/2;++i){\n",
"\t\tint a,b,w;\n",
"\t\tscanf(\"%d%d%d\",&a,&b,&w);\n",
"\t\tGraph[a][b] = Graph[b][a] = w;\n",
"\t}\n",
"\t\n",
"\treturn true;\n",
"}\n",
"\n",
"int main(){\n",
"\twhile( read() ){\n",
"\t\tprintf(\"%d\\n\",Prim());\n",
"\t}\n",
"\treturn 0;\n",
"}\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"#include <cstdio>\n",
"#include <algorithm>\n",
"using namespace std;\n",
"\n",
"typedef int weight_t; \n",
"\n",
"#define SIZE 101\n",
"\n",
"//并查集结构\n",
"int Father[SIZE];\n",
"void init(int n){for(int i=0;i<=n;Father[i]=i++);}\n",
"int find(int x){return Father[x]==x?x:Father[x]=find(Father[x]);}\n",
"void unite(int x,int y){Father[find(y)]=Father[find(x)];}\n",
"\n",
"int N;\n",
"\n",
"//边结构\n",
"struct edge_t{\n",
"\tint s;\n",
"\tint e;\n",
"\tweight_t w;\n",
"}Edge[SIZE*SIZE/2];\n",
"int ECnt = 0;\n",
"\n",
"//重载，用于边排序\n",
"bool operator < (edge_t const&lhs,edge_t const&rhs){\n",
"\tif ( lhs.w != rhs.w ) return lhs.w < rhs.w;\n",
"\tif ( lhs.s != rhs.s ) return lhs.s < rhs.s;\n",
"\treturn lhs.e < rhs.e;\n",
"}\n",
"\n",
"//生成边\n",
"inline void mkEdge(int a,int b,weight_t w){\n",
"\tif ( a > b ) swap(a,b);\n",
"\n",
"\tEdge[ECnt].s = a;\n",
"\tEdge[ECnt].e = b;\n",
"\tEdge[ECnt++].w = w;\n",
"}\n",
"\n",
"//Kruskal算法，vn是点的数量，en是边的数量，返回MST的长度\n",
"weight_t Kruskal(int vn,int en){\n",
"\tinit(vn);//并查集初始化\n",
"\tsort(Edge,Edge+en);//边排序\n",
"\n",
"\tweight_t ans = 0;\n",
"\tfor(int i=0;i<en;++i){\n",
"\t\t//该边已存在于MST中\n",
"\t\tif ( find(Edge[i].s) == find(Edge[i].e) )\n",
"\t\t\tcontinue;\n",
"\n",
"\t\t//将该边加入MST\n",
"\t\tans += Edge[i].w;\n",
"\t\tunite(Edge[i].s,Edge[i].e);\n",
"\t\t--vn;\n",
"\n",
"\t\t//MST已完全生成\n",
"\t\tif ( 1 == vn ) break;\n",
"\t}\n",
"\n",
"\treturn ans;\n",
"}\n",
"\n",
"bool read(){\n",
"\tscanf(\"%d\",&N);\n",
"\tif ( 0 == N ) return false;\n",
"\t\n",
"\tECnt = 0;\n",
"\tfor(int i=0;i<N*(N-1)/2;++i){\n",
"\t\tint a,b,w;\n",
"\t\tscanf(\"%d%d%d\",&a,&b,&w);\n",
"\t\tmkEdge(a,b,w);\n",
"\t}\n",
"\t\n",
"\treturn true;\n",
"}\n",
"\n",
"int main(){\n",
"\twhile( read() ){\n",
"\t\tprintf(\"%d\\n\",Kruskal(N,ECnt));\n",
"\t}\n",
"\treturn 0;\n",
"}"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "C",
"language": "c",
"name": "c"
},
"language_info": {
"file_extension": ".c",
"mimetype": "text/plain",
"name": "c"
}
},
"nbformat": 4,
"nbformat_minor": 4
}