mirror of
https://github.com/tencentmusic/cube-studio.git
synced 2024-11-27 05:33:10 +08:00
Add Machine Learning Algorithm Files(Part 1 of 4)
Some Jupyter Machine Learning Algorithm File 1 of 4
This commit is contained in:
parent
3a14027296
commit
e5deba0845
109
aihub/machine-learning/关联分析 (有趣).ipynb
Normal file
109
aihub/machine-learning/关联分析 (有趣).ipynb
Normal file
@ -0,0 +1,109 @@
|
||||
{
|
||||
"cells": [
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 关联规则不一定都是有趣"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"例如,一个谷类早餐的零售商对 5000 名 学生的调查的案例。 用来研究是否在学生打完篮球后向学生推荐早餐。\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"数据表明: \n",
|
||||
"\n",
|
||||
"60%的学生早上会先打篮球\n",
|
||||
"\n",
|
||||
"75%的学生吃这类早餐(包含打篮球后吃早餐的和不打篮球直接吃早餐的)\n",
|
||||
"\n",
|
||||
"40% 的学生既打篮球又吃这类早餐"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"假设支持度阈值 s=0.4,置信度阈值 c=60%。基于上面数据和假设我们可挖掘出强关联规则“(打篮球)→(吃早餐)”"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"因为其(打篮球) 和(吃早餐)的支持度都大于支持度阈值,都是频繁项,而规则的置信度 $c=\\frac{40\\%}{60\\%}=66.6\\%$也大于置信度阈值。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"\f",
|
||||
"然而,以上的关联规则很容易产生误解,因为吃早餐的比例为 75%,大于 66%。 "
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"也就是说,本来不打篮球先选择吃这种早餐的概率大于75%,但是打完篮球的学生就不想吃这种早餐或者不吃早餐了。\n",
|
||||
"\n",
|
||||
"因为打球后的学生吃这种早餐的概率降到了66%。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"所以打篮球与吃早餐实际上是负关联的。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**所以强关联不一定是有趣的。**\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"\n",
|
||||
"我们应该使用 **相关性度量**(这里使用提升读度量)来表征关联提升。\n",
|
||||
"\n",
|
||||
"也就是$P(B/A)/P(B)$来表示**在A出现的情况下推荐B是否比没出现A之前推荐B更好。**\n",
|
||||
"\n",
|
||||
"公式等价于$lift(A,B)=\\frac{P( A\\bigcup B)}{P(A)P(B)}$"
|
||||
]
|
||||
}
|
||||
],
|
||||
"metadata": {
|
||||
"kernelspec": {
|
||||
"display_name": "Python 3",
|
||||
"language": "python",
|
||||
"name": "python3"
|
||||
},
|
||||
"language_info": {
|
||||
"codemirror_mode": {
|
||||
"name": "ipython",
|
||||
"version": 3
|
||||
},
|
||||
"file_extension": ".py",
|
||||
"mimetype": "text/x-python",
|
||||
"name": "python",
|
||||
"nbconvert_exporter": "python",
|
||||
"pygments_lexer": "ipython3",
|
||||
"version": "3.6.9"
|
||||
}
|
||||
},
|
||||
"nbformat": 4,
|
||||
"nbformat_minor": 4
|
||||
}
|
||||
416
aihub/machine-learning/关联分析(Apriori).ipynb
Normal file
416
aihub/machine-learning/关联分析(Apriori).ipynb
Normal file
@ -0,0 +1,416 @@
|
||||
{
|
||||
"cells": [
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 关联分析的基本概念"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"关联分析(Association Analysis):在大规模数据集中寻找有趣的关系。\n",
|
||||
"\n",
|
||||
"频繁项集(Frequent Item Sets):经常出现在一块的物品的集合,即包含0个或者多个项的集合称为项集。\n",
|
||||
"\n",
|
||||
"支持度(Support):数据集中包含该项集的记录所占的比例,是针对项集来说的。\n",
|
||||
"\n",
|
||||
"置信度(Confidence):出现某些物品时,另外一些物品必定出现的概率,针对规则而言。\n",
|
||||
"\n",
|
||||
"关联规则(Association Rules):暗示两个物品之间可能存在很强的关系。形如A->B的表达式,规则A->B的度量包括支持度和置信度\n",
|
||||
"\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"#### 项集支持度:一个项集出现的次数与数据集所有事物数的百分比称为项集的支持度\n",
|
||||
"\n",
|
||||
"$eg: support(A\\Rightarrow B) = support\\_count(A∪ B) / N$"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
">支持度反映了A和B同时出现的概率,关联规则的支持度等于频繁集的支持度。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"#### 项集置信度:包含A的数据集中包含B的百分比\n",
|
||||
"\n",
|
||||
"$eg: confidence(A\\Rightarrow B) = support\\_count(A∪B ) / support\\_count(A)$"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
">置信度反映了如果交易中包含A,则交易包含B的概率。也可以称为在A发生的条件下,发生B的概率,成为条件概率。\n",
|
||||
"\n",
|
||||
"**只有支持度和置信度(可信度)较高的关联规则才是用户感兴趣的。**"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 关联分析步骤\n",
|
||||
"\n",
|
||||
"1、发现频繁项集,即计算所有可能组合数的支持度,找出不少于人为设定的最小支持度的集合。\n",
|
||||
"\n",
|
||||
"2、发现关联规则,即计算不小于人为设定的最小支持度的集合的置信度,找到不小于认为设定的最小置信度规则。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 关联分析的两种关系:简单关联关系和序列关联关系\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"**简单关联关系:**\n",
|
||||
"\n",
|
||||
"简单关联关系可以从经典的购物中进行分析,购买面包的顾客80%都会购买牛奶,由于面包和牛奶是早餐搭配的必需品,二者搭配构成了早餐的组成部分,这就是一种简单的关联关系。\n",
|
||||
"\n",
|
||||
"**序列关联关系:**\n",
|
||||
"\n",
|
||||
"当购买一款新手机后,就会考虑去购买手机膜等手机配件,这就是一种序列关系,不会先买手机膜再买手机的,先后关系是非常明显的,这种关系是一种顺序性的关系,也就是一种序列关联关系。\n",
|
||||
"\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
">关联规则:规则就是一种衡量事物的标准,也就是一个算法。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 简单关联规则算法\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"**算法思想基础**\n",
|
||||
"\n",
|
||||
"> 如果某个项集是频繁的,那么它的所有子集也是频繁的。更常用的是它的逆否命题,即如果一个项集是非频繁的,那么它的所有超集也是非频繁的。\n",
|
||||
"\n",
|
||||
"简单关联规则是无指导的学习方法,着重探索内部结构。\n",
|
||||
"\n",
|
||||
"简单关联规则也是使用最多的技术,主要算法包括:Apriori、GRI、Carma,其中Apriori和Carma主要是如何提高关联规则的分析效率,而GRI注重如何将单一概念层次的关联推广到更多概念层次的关联,进而揭示事物内在结构。\n",
|
||||
"\n",
|
||||
"简单关联规则的数据存储形式:**一种是交易数据格式,一种是表格数据格式。**"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 序列关联规则算法\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"序列关联规则的核心就是找到事物发展的前后关联性,研究序列关联可以来推测事物未来的发展情况,并根据预测的发展情况进行事物的分配和安排。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 如何设定合理的支持度和置信度?\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"对于某条规则:"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"$(A=a)->(B=b)$(support=30%,confident=60%)"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"其中:support=30%表示在所有的数据记录中,同时出现A=a和B=b的概率为30%;confident=60%表示在所有的数据记录中,在出现A=a的情况下出现B=b的概率为60%,也就是条件概率。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"支持度揭示了A=a和B=b同时出现的概率,置信度揭示了当A=a出现时,B=b是否会一定出现的概率。\n",
|
||||
"\n",
|
||||
"(1)如果支持度和置信度闭值设置的过高,虽然可以减少挖掘时间,但是容易造成一些隐含在数据中非频繁特征项被忽略掉,难以发现足够有用的规则;\n",
|
||||
"\n",
|
||||
"(2)如果支持度和置信度闭值设置的过低,又有可能产生过多的规则,甚至产生大量冗余和无效的规则,同时由于算法存在的固有问题,会导致高负荷的计算量,大大增加挖掘时间。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 关联分析的应用\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"(1):购物篮分析,通过查看那些商品经常在一起出售,可以帮助商店了解用户的购物行为,这种从数据的海洋中抽取只是可以用于商品定价、市场促销、存货管理等环节\n",
|
||||
"\n",
|
||||
"(2):在Twitter源中发现一些公共词。对于给定的搜索词,发现推文中频繁出现的单词集合\n",
|
||||
"\n",
|
||||
"(3):从新闻网站点击流中挖掘新闻流行趋势,挖掘哪些新闻广泛被用户浏览到\n",
|
||||
"\n",
|
||||
"(4):搜索引擎推荐,在用户输入查询时推荐同时相关的查询词项\n",
|
||||
"\n",
|
||||
"(5):发现毒蘑菇的相似特征。这里只对包含某个特征元素(有毒素)的项集感兴趣,从中寻找毒蘑菇中的一些公共特征,利用这些特征来避免迟到哪些有毒的蘑菇\n",
|
||||
"\n",
|
||||
"(6):图书馆信息的书籍推荐,对于学生的借书信息,不同专业学生的借书情况,来挖掘不同学生的借书情况,进行数目的推荐。\n",
|
||||
"\n",
|
||||
"(7):校园网新闻通知信息的推荐,在对校园网新闻通知信息进行挖掘的过程中,分析不同部门,不同学院的新闻信息的不同,在进行新闻信息浏览的过程中进行新闻的推荐。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# Apriori算法\n",
|
||||
"\n",
|
||||
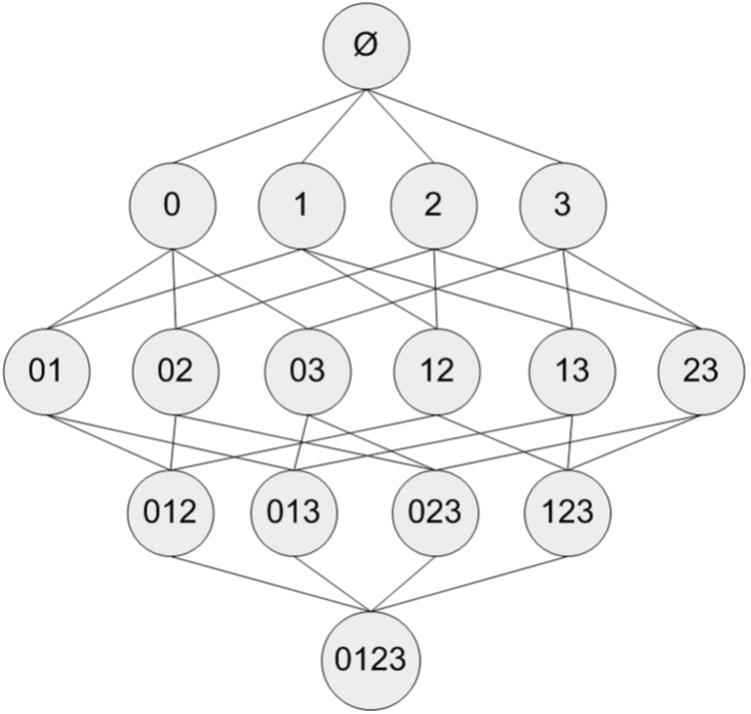
"假设我们有一家经营着4种商品(商品0,商品1,商品2和商品3)的杂货店,图显示了所有商品之间所有的可能组合:\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"对于单个项集的支持度,我们可以通过遍历每条记录并检查该记录是否包含该项集来计算。\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"对于包含N中物品的数据集共有$2^N−1$种项集组合,重复上述计算过程是不现实的。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"研究人员通过这个假设,发现了一种所谓的Apriori原理,可以帮助我们减少计算量。\n",
|
||||
"\n",
|
||||
">Apriori原理是说如果某个项集是频繁的,那么它的所有子集也是频繁的。\n",
|
||||
"\n",
|
||||
">**例如一个频繁项集包含3个项A、B、C,则这三个项组成的子集{A},{B},{C},{A、B},{A、C}、{B、C}一定是频繁项集。**"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"不过更常用的是它的逆否命题,即如果一个项集是非频繁的,那么它的所有超集也是非频繁的。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
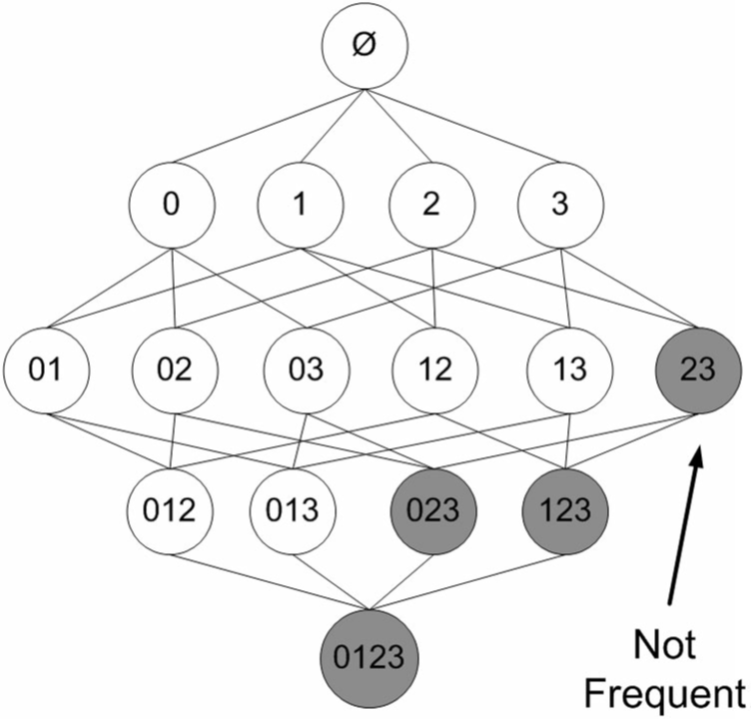
"在图中,已知阴影项集{2,3}是非频繁的。利用这个知识,我们就知道项集{0,2,3},{1,2,3}以及{0,1,2,3}也是非频繁的。\n",
|
||||
"\n",
|
||||
"也就是说,一旦计算出了{2,3}的支持度,知道它是非频繁的后,就可以紧接着排除{0,2,3}、{1,2,3}和{0,1,2,3}。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
""
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
">Apriori算法是发现**频繁项集**的一种方法。并不会找出关联规则,关联规则需要在找到频繁项集以后我们再来统计。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"### Apriori算法的两个输入参数分别是最小支持度和数据集。\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"该算法首先会生成所有单个元素的项集列表。\n",
|
||||
"\n",
|
||||
"接着扫描数据集来查看哪些项集满足最小支持度要求,那些不满足最小支持度的集合会被去掉。\n",
|
||||
"\n",
|
||||
"然后,对剩下来的集合进行组合以生成包含两个元素的项集。\n",
|
||||
"\n",
|
||||
"接下来,再重新扫描交易记录,去掉不满足最小支持度的项集。该过程重复进行直到所有项集都被去掉。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"该算法需要不断寻找候选集,然后剪枝即去掉非频繁子集的候选集,时间复杂度由暴力枚举所有子集的指数级别$O(n^2)$降为多项式级别,"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"\n",
|
||||
"### Ariori算法有两个主要步骤:\n",
|
||||
"\n",
|
||||
"1、连接:(将项集进行两两连接形成新的候选集)\n",
|
||||
"\n",
|
||||
"利用已经找到的$k$个项的频繁项集$L_k$,通过两两连接得出候选集$C_{k+1}$,注意进行连接的$L_k[i]$,$L_k[j]$,必须有$k-1个$属性值相同,然后另外两个不同的分别分布在$L_k[i]$,$L_k[j]$中,这样的求出的$C_{k+1}$为$L_{k+1}$的候选集。\n",
|
||||
"\n",
|
||||
"2、剪枝:(去掉非频繁项集)\n",
|
||||
"\n",
|
||||
"候选集 $C_{k+1}$中的并不都是频繁项集,必须剪枝去掉,越早越好以防止所处理的数据无效项越来越多。\n",
|
||||
"\n",
|
||||
"**只有当子集都是频繁集的候选集才是频繁集,这是剪枝的依据**。\n",
|
||||
" "
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"```\n",
|
||||
"算法实现\n",
|
||||
"```\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": 1,
|
||||
"metadata": {},
|
||||
"outputs": [
|
||||
{
|
||||
"name": "stdout",
|
||||
"output_type": "stream",
|
||||
"text": [
|
||||
"[[frozenset({5}), frozenset({2}), frozenset({3})], [frozenset({2, 5})], []] {frozenset({1}): 0.5, frozenset({3}): 0.75, frozenset({4}): 0.25, frozenset({2}): 0.75, frozenset({5}): 0.75, frozenset({2, 5}): 0.75, frozenset({3, 5}): 0.5, frozenset({2, 3}): 0.5}\n"
|
||||
]
|
||||
}
|
||||
],
|
||||
"source": [
|
||||
"from numpy import *\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"def loadDataSet():\n",
|
||||
" return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]\n",
|
||||
"\n",
|
||||
"# 获取候选1项集,dataSet为事务集。返回一个list,每个元素都是set集合\n",
|
||||
"def createC1(dataSet):\n",
|
||||
" C1 = [] # 元素个数为1的项集(非频繁项集,因为还没有同最小支持度比较)\n",
|
||||
" for transaction in dataSet:\n",
|
||||
" for item in transaction:\n",
|
||||
" if not [item] in C1:\n",
|
||||
" C1.append([item])\n",
|
||||
" C1.sort() # 这里排序是为了,生成新的候选集时可以直接认为两个n项候选集前面的部分相同\n",
|
||||
" # 因为除了候选1项集外其他的候选n项集都是以二维列表的形式存在,所以要将候选1项集的每一个元素都转化为一个单独的集合。\n",
|
||||
" return list(map(frozenset, C1)) #map(frozenset, C1)的语义是将C1由Python列表转换为不变集合(frozenset,Python中的数据结构)\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"# 找出候选集中的频繁项集\n",
|
||||
"# dataSet为全部数据集,Ck为大小为k(包含k个元素)的候选项集,minSupport为设定的最小支持度\n",
|
||||
"def scanD(dataSet, Ck, minSupport):\n",
|
||||
" ssCnt = {} # 记录每个候选项的个数\n",
|
||||
" for tid in dataSet:\n",
|
||||
" for can in Ck:\n",
|
||||
" if can.issubset(tid):\n",
|
||||
" ssCnt[can] = ssCnt.get(can, 0) + 1 # 计算每一个项集出现的频率\n",
|
||||
" numItems = float(len(dataSet))\n",
|
||||
" retList = []\n",
|
||||
" supportData = {}\n",
|
||||
" for key in ssCnt:\n",
|
||||
" support = ssCnt[key] / numItems\n",
|
||||
" if support >= minSupport:\n",
|
||||
" retList.insert(0, key) #将频繁项集插入返回列表的首部\n",
|
||||
" supportData[key] = support\n",
|
||||
" return retList, supportData #retList为在Ck中找出的频繁项集(支持度大于minSupport的),supportData记录各频繁项集的支持度\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"# 通过频繁项集列表Lk和项集个数k生成候选项集C(k+1)。\n",
|
||||
"def aprioriGen(Lk, k):\n",
|
||||
" retList = []\n",
|
||||
" lenLk = len(Lk)\n",
|
||||
" for i in range(lenLk):\n",
|
||||
" for j in range(i + 1, lenLk):\n",
|
||||
" # 前k-1项相同时,才将两个集合合并,合并后才能生成k+1项\n",
|
||||
" L1 = list(Lk[i])[:k-2]; L2 = list(Lk[j])[:k-2] # 取出两个集合的前k-1个元素\n",
|
||||
" L1.sort(); L2.sort()\n",
|
||||
" if L1 == L2:\n",
|
||||
" retList.append(Lk[i] | Lk[j])\n",
|
||||
" return retList\n",
|
||||
"\n",
|
||||
"# 获取事务集中的所有的频繁项集\n",
|
||||
"# Ck表示项数为k的候选项集,最初的C1通过createC1()函数生成。Lk表示项数为k的频繁项集,supK为其支持度,Lk和supK由scanD()函数通过Ck计算而来。\n",
|
||||
"def apriori(dataSet, minSupport=0.5):\n",
|
||||
" C1 = createC1(dataSet) # 从事务集中获取候选1项集\n",
|
||||
" D = list(map(set, dataSet)) # 将事务集的每个元素转化为集合\n",
|
||||
" L1, supportData = scanD(D, C1, minSupport) # 获取频繁1项集和对应的支持度\n",
|
||||
" L = [L1] # L用来存储所有的频繁项集\n",
|
||||
" k = 2\n",
|
||||
" while (len(L[k-2]) > 0): # 一直迭代到项集数目过大而在事务集中不存在这种n项集\n",
|
||||
" Ck = aprioriGen(L[k-2], k) # 根据频繁项集生成新的候选项集。Ck表示项数为k的候选项集\n",
|
||||
" Lk, supK = scanD(D, Ck, minSupport) # Lk表示项数为k的频繁项集,supK为其支持度\n",
|
||||
" L.append(Lk);supportData.update(supK) # 添加新频繁项集和他们的支持度\n",
|
||||
" k += 1\n",
|
||||
" return L, supportData\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"if __name__=='__main__':\n",
|
||||
" dataSet = loadDataSet() # 获取事务集。每个元素都是列表\n",
|
||||
" # C1 = createC1(dataSet) # 获取候选1项集。每个元素都是集合\n",
|
||||
" # D = list(map(set, dataSet)) # 转化事务集的形式,每个元素都转化为集合。\n",
|
||||
" # L1, suppDat = scanD(D, C1, 0.5)\n",
|
||||
" # print(L1,suppDat)\n",
|
||||
"\n",
|
||||
"\n",
|
||||
" L, suppData = apriori(dataSet,minSupport=0.7)\n",
|
||||
" print(L,suppData)"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": []
|
||||
}
|
||||
],
|
||||
"metadata": {
|
||||
"kernelspec": {
|
||||
"display_name": "Python 3",
|
||||
"language": "python",
|
||||
"name": "python3"
|
||||
},
|
||||
"language_info": {
|
||||
"codemirror_mode": {
|
||||
"name": "ipython",
|
||||
"version": 3
|
||||
},
|
||||
"file_extension": ".py",
|
||||
"mimetype": "text/x-python",
|
||||
"name": "python",
|
||||
"nbconvert_exporter": "python",
|
||||
"pygments_lexer": "ipython3",
|
||||
"version": "3.6.9"
|
||||
}
|
||||
},
|
||||
"nbformat": 4,
|
||||
"nbformat_minor": 4
|
||||
}
|
||||
593
aihub/machine-learning/关联分析(FP-grow).ipynb
Normal file
593
aihub/machine-learning/关联分析(FP-grow).ipynb
Normal file
@ -0,0 +1,593 @@
|
||||
{
|
||||
"cells": [
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# FP-growth算法来高效发现频繁项集"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"### FP树:用于编码数据集的有效方式"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"FP-growth算法将数据存储在一种称为FP树的紧凑数据结构中。\n",
|
||||
"\n",
|
||||
"FP代表频繁模式(Frequent Pattern)。\n",
|
||||
"\n",
|
||||
"一棵FP树看上去与计算机科学中的其他树结构类似,但是它通过链接(link)来连接相似元素,被连起来的元素项可以看成一个链表。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"与搜索树不同的是,一个元素项可以在一棵FP树种出现多次。\n",
|
||||
"\n",
|
||||
"FP树会存储项集的出现频率,而每个项集会以路径的方式存储在数中。 \n",
|
||||
"\n",
|
||||
"树节点上给出集合中的单个元素及其在序列中的出现次数,路径会给出该序列的出现次数。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"相似项之间的链接称为节点链接(node link),用于快速发现相似项的位置。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**下图给出了FP树的一个例子**\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"```\n",
|
||||
"事务集\n",
|
||||
"```"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"| 事务ID | 事务中的元素项 | \n",
|
||||
"| -------- | ----- | \n",
|
||||
"|001\t|r, z, h, j, p|\n",
|
||||
"|002|\tz, y, x, w, v, u, t, s|\n",
|
||||
"|003\t|z|\n",
|
||||
"|004|\tr, x, n, o, s|\n",
|
||||
"|005\t|y, r, x, z, q, t, p|\n",
|
||||
"|006\t|y, z, x, e, q, s, t, m|"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"```\n",
|
||||
"生成的FP树为\n",
|
||||
"```\n",
|
||||
"\n",
|
||||
"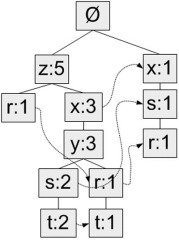"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**对FP树的解读:**"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"图中,元素项z出现了5次,集合{r, z}出现了1次。\n",
|
||||
"\n",
|
||||
"于是可以得出结论:z一定是自己本身或者和其他符号一起出现了4次。\n",
|
||||
"\n",
|
||||
"集合{t, s, y, x, z}出现了2次,集合{t, r, y, x, z}出现了1次,z本身单独出现1次。\n",
|
||||
"\n",
|
||||
"就像这样,FP树的解读方式是读取某个节点开始到根节点的路径。\n",
|
||||
"\n",
|
||||
"路径上的元素构成一个频繁项集,开始节点的值表示这个项集的支持度。\n",
|
||||
"\n",
|
||||
"根据图,我们可以快速读出项集{z}的支持度为5、项集{t, s, y, x, z}的支持度为2、项集{r, y, x, z}的支持度为1、项集{r, s, x}的支持度为1。\n",
|
||||
"\n",
|
||||
"FP树中会多次出现相同的元素项,也是因为同一个元素项会存在于多条路径,构成多个频繁项集。\n",
|
||||
"\n",
|
||||
"但是频繁项集的共享路径是会合并的,如图中的{t, s, y, x, z}和{t, r, y, x, z}"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"和之前一样,我们取一个最小阈值,出现次数低于最小阈值的元素项将被直接忽略。图中将最小支持度设为3,所以q和p没有在FP中出现。\n",
|
||||
"\n",
|
||||
"**FP-growth算法的工作流程如下:**\n",
|
||||
"\n",
|
||||
"首先构建FP树,然后利用它来挖掘频繁项集。\n",
|
||||
"\n",
|
||||
"为构建FP树,需要对原始数据集扫描两遍。\n",
|
||||
"\n",
|
||||
"第一遍对所有元素项的出现次数进行计数。\n",
|
||||
"\n",
|
||||
"数据库的第一遍扫描用来统计出现的频率,而第二遍扫描中只考虑那些频繁元素。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**FP-growth算法发现频繁项集的基本过程如下:**\n",
|
||||
"\n",
|
||||
" - 构建FP树 \n",
|
||||
" - 从FP树中挖掘频繁项集 "
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**头指针表**\n",
|
||||
"\n",
|
||||
"FP-growth算法还需要一个称为头指针表的数据结构,其实很简单,就是用来记录各个元素项的总出现次数的数组,再附带一个指针指向FP树中该元素项的第一个节点。这样每个元素项都构成一条单链表。\n",
|
||||
"\n",
|
||||
"图示说明:\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"\n",
|
||||
"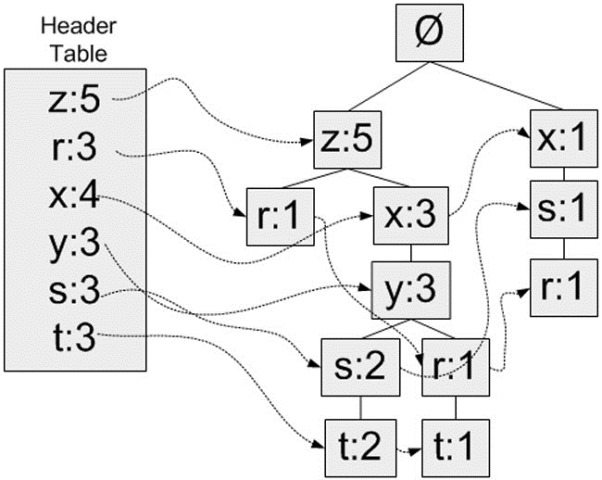\n",
|
||||
"\n",
|
||||
"这里使用Python字典作为数据结构,来保存头指针表。以元素项名称为键,保存出现的总次数和一个指向第一个相似元素项的指针。\n",
|
||||
"\n",
|
||||
"第一次遍历数据集会获得每个元素项的出现频率,去掉不满足最小支持度的元素项,生成这个头指针表。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**元素项排序**\n",
|
||||
"\n",
|
||||
"上文提到过,FP树会合并相同的频繁项集(或相同的部分)。\n",
|
||||
"\n",
|
||||
"因此为判断两个项集的相似程度需要对项集中的元素进行排序(不过原因也不仅如此,还有其它好处)。\n",
|
||||
"\n",
|
||||
"排序基于元素项的绝对出现频率(总的出现次数)来进行。\n",
|
||||
"\n",
|
||||
"在第二次遍历数据集时,会读入每个项集(读取),去掉不满足最小支持度的元素项(过滤),然后对元素进行排序(重排序)。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
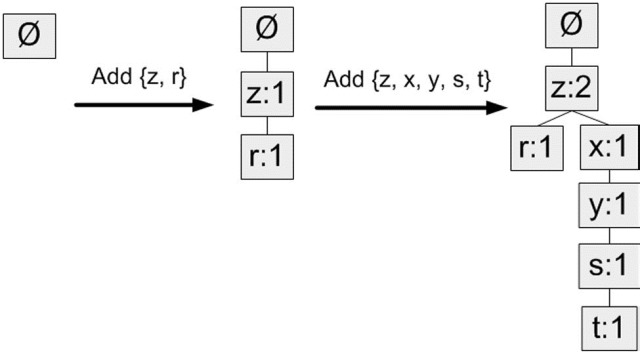
"source": [
|
||||
"**构建FP树**\n",
|
||||
"\n",
|
||||
"在对事务记录过滤和排序之后,就可以构建FP树了。\n",
|
||||
"\n",
|
||||
"从空集开始,将过滤和重排序后的频繁项集一次添加到树中。如果树中已存在现有元素,则增加现有元素的值;如果现有元素不存在,则向树添加一个分支。\n",
|
||||
"\n",
|
||||
"对前两条事务进行添加的过程:\n",
|
||||
"\n",
|
||||
""
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**实现流程**\n",
|
||||
"\n",
|
||||
"输入:数据集、最小值尺度\n",
|
||||
"输出:FP树、头指针表\n",
|
||||
"\n",
|
||||
" - 1、遍历数据集,统计各元素项出现次数,创建头指针表\n",
|
||||
" - 2、移除头指针表中不满足最小值尺度的元素项\n",
|
||||
" - 3、第二次遍历数据集,创建FP树。对每个数据集中的项集:\n",
|
||||
" - 3.1 初始化空FP树\n",
|
||||
" - 3.2 对每个项集进行过滤和重排序\n",
|
||||
" - 3.3 使用这个项集更新FP树,从FP树的根节点开始:\n",
|
||||
" - 3.3.1 如果当前项集的第一个元素项存在于FP树当前节点的子节点中,则更新这个子节点的计数值\n",
|
||||
" - 3.3.2 否则,创建新的子节点,更新头指针表\n",
|
||||
" - 3.3.3 对当前项集的其余元素项和当前元素项的对应子节点递归3.3的过程\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**从一棵FP树种挖掘频繁项集**\n",
|
||||
"\n",
|
||||
"从FP树中抽取频繁项集的三个基本步骤如下:\n",
|
||||
"\n",
|
||||
" - 从FP树中获得条件模式基; \n",
|
||||
" - 利用条件模式基,构建一个条件FP树; \n",
|
||||
" - 迭代重复步骤1步骤2,直到树包含一个元素项为止。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"其中“条件模式基”是以所查找元素项为结尾的路径集合。每一条路径其实都是一条前缀路径(prefix path)。\n",
|
||||
"\n",
|
||||
"简而言之,一条前缀路径是介于所查找元素项与树根节点之间的所有内容。\n",
|
||||
"\n",
|
||||
"例如\n",
|
||||
"\n",
|
||||
"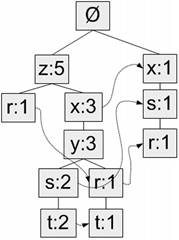"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"则每一个频繁元素项的条件模式基为:\n",
|
||||
"\n",
|
||||
"| 频繁项 | 前缀路径 |\n",
|
||||
"| ----| ----|\n",
|
||||
"|z|\t{}: 5|\n",
|
||||
"|r|{x, s}: 1, {z, x, y}: 1, {z}: 1|\n",
|
||||
"|x|\t{z}: 3, {}: 1|\n",
|
||||
"|y|\t{z, x}: 3|\n",
|
||||
"|s|\t{z, x, y}: 2, {x}: 1|\n",
|
||||
"|t|\t{z, x, y, s}: 2, {z, x, y, r}: 1|"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"发现规律了吗,z存在于路径{z}中,因此前缀路径为空,另添加一项该路径中z节点的计数值5构成其条件模式基;\n",
|
||||
"\n",
|
||||
"r存在于路径{r, z}、{r, y, x, z}、{r, s, x}中,分别获得前缀路径{z}、{y, x, z}、{s, x},另添加对应路径中r节点的计数值(均为1)构成r的条件模式基;\n",
|
||||
"\n",
|
||||
"以此类推。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**创建条件FP树**\n",
|
||||
"\n",
|
||||
"对于每一个频繁项,都要创建一棵条件FP树。可以使用刚才发现的条件模式基作为输入数据,并通过相同的建树代码来构建这些树。\n",
|
||||
"\n",
|
||||
"例如\n",
|
||||
"\n",
|
||||
">对于r,即以“{x, s}: 1, {z, x, y}: 1, {z}: 1”为输入,调用函数createTree()获得r的条件FP树;\n",
|
||||
"\n",
|
||||
">对于t,输入是对应的条件模式基“{z, x, y, s}: 2, {z, x, y, r}: 1”。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**递归查找频繁项集**\n",
|
||||
" \n",
|
||||
"有了FP树和条件FP树,我们就可以在前两步的基础上递归得查找频繁项集。\n",
|
||||
"\n",
|
||||
"递归的过程是这样的:\n",
|
||||
"输入:我们有当前数据集的FP树(inTree,headerTable)\n",
|
||||
"\n",
|
||||
" - 1、初始化一个空列表preFix表示前缀\n",
|
||||
" - 2、初始化一个空列表freqItemList接收生成的频繁项集(作为输出)\n",
|
||||
" - 3、对headerTable中的每个元素basePat(按计数值由小到大),递归:\n",
|
||||
" - 3.1 记basePat + preFix为当前频繁项集newFreqSet\n",
|
||||
" - 3.2 将newFreqSet添加到freqItemList中\n",
|
||||
" - 3.3 计算t的条件FP树(myCondTree、myHead)\n",
|
||||
" - 3.4 当条件FP树不为空时,继续下一步;否则退出递归\n",
|
||||
" - 3.5 以myCondTree、myHead为新的输入,以newFreqSet为新的preFix,外加freqItemList,递归这个过程"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**实现代码**"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": 1,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"# FP树类\n",
|
||||
"class treeNode:\n",
|
||||
" def __init__(self, nameValue, numOccur, parentNode):\n",
|
||||
" self.name = nameValue #节点元素名称,在构造时初始化为给定值\n",
|
||||
" self.count = numOccur # 出现次数,在构造时初始化为给定值\n",
|
||||
" self.nodeLink = None # 指向下一个相似节点的指针,默认为None\n",
|
||||
" self.parent = parentNode # 指向父节点的指针,在构造时初始化为给定值\n",
|
||||
" self.children = {} # 指向子节点的字典,以子节点的元素名称为键,指向子节点的指针为值,初始化为空字典\n",
|
||||
"\n",
|
||||
" # 增加节点的出现次数值\n",
|
||||
" def inc(self, numOccur):\n",
|
||||
" self.count += numOccur\n",
|
||||
"\n",
|
||||
" # 输出节点和子节点的FP树结构\n",
|
||||
" def disp(self, ind=1):\n",
|
||||
" print(' ' * ind, self.name, ' ', self.count)\n",
|
||||
" for child in self.children.values():\n",
|
||||
" child.disp(ind + 1)\n",
|
||||
"\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": 2,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"# =======================================================构建FP树==================================================\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"# 对不是第一个出现的节点,更新头指针块。就是添加到相似元素链表的尾部\n",
|
||||
"def updateHeader(nodeToTest, targetNode):\n",
|
||||
" while (nodeToTest.nodeLink != None):\n",
|
||||
" nodeToTest = nodeToTest.nodeLink\n",
|
||||
" nodeToTest.nodeLink = targetNode\n",
|
||||
"\n",
|
||||
"# 根据一个排序过滤后的频繁项更新FP树\n",
|
||||
"def updateTree(items, inTree, headerTable, count):\n",
|
||||
" if items[0] in inTree.children:\n",
|
||||
" # 有该元素项时计数值+1\n",
|
||||
" inTree.children[items[0]].inc(count)\n",
|
||||
" else:\n",
|
||||
" # 没有这个元素项时创建一个新节点\n",
|
||||
" inTree.children[items[0]] = treeNode(items[0], count, inTree)\n",
|
||||
" # 更新头指针表或前一个相似元素项节点的指针指向新节点\n",
|
||||
" if headerTable[items[0]][1] == None: # 如果是第一次出现,则在头指针表中增加对该节点的指向\n",
|
||||
" headerTable[items[0]][1] = inTree.children[items[0]]\n",
|
||||
" else:\n",
|
||||
" updateHeader(headerTable[items[0]][1], inTree.children[items[0]])\n",
|
||||
"\n",
|
||||
" if len(items) > 1:\n",
|
||||
" # 对剩下的元素项迭代调用updateTree函数\n",
|
||||
" updateTree(items[1::], inTree.children[items[0]], headerTable, count)\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"# 主程序。创建FP树。dataSet为事务集,为一个字典,键为每个事物,值为该事物出现的次数。minSup为最低支持度\n",
|
||||
"def createTree(dataSet, minSup=1):\n",
|
||||
" # 第一次遍历数据集,创建头指针表\n",
|
||||
" headerTable = {}\n",
|
||||
" for trans in dataSet:\n",
|
||||
" for item in trans:\n",
|
||||
" headerTable[item] = headerTable.get(item, 0) + dataSet[trans]\n",
|
||||
" # 移除不满足最小支持度的元素项\n",
|
||||
" keys = list(headerTable.keys()) # 因为字典要求在迭代中不能修改,所以转化为列表\n",
|
||||
" for k in keys:\n",
|
||||
" if headerTable[k] < minSup:\n",
|
||||
" del(headerTable[k])\n",
|
||||
" # 空元素集,返回空\n",
|
||||
" freqItemSet = set(headerTable.keys())\n",
|
||||
" if len(freqItemSet) == 0:\n",
|
||||
" return None, None\n",
|
||||
" # 增加一个数据项,用于存放指向相似元素项指针\n",
|
||||
" for k in headerTable:\n",
|
||||
" headerTable[k] = [headerTable[k], None] # 每个键的值,第一个为个数,第二个为下一个节点的位置\n",
|
||||
" retTree = treeNode('Null Set', 1, None) # 根节点\n",
|
||||
" # 第二次遍历数据集,创建FP树\n",
|
||||
" for tranSet, count in dataSet.items():\n",
|
||||
" localD = {} # 记录频繁1项集的全局频率,用于排序\n",
|
||||
" for item in tranSet:\n",
|
||||
" if item in freqItemSet: # 只考虑频繁项\n",
|
||||
" localD[item] = headerTable[item][0] # 注意这个[0],因为之前加过一个数据项\n",
|
||||
" if len(localD) > 0:\n",
|
||||
" orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: p[1], reverse=True)] # 排序\n",
|
||||
" updateTree(orderedItems, retTree, headerTable, count) # 更新FP树\n",
|
||||
" return retTree, headerTable\n",
|
||||
"\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": 3,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"# =================================================查找元素条件模式基===============================================\n",
|
||||
"\n",
|
||||
"# 直接修改prefixPath的值,将当前节点leafNode添加到prefixPath的末尾,然后递归添加其父节点。\n",
|
||||
"# prefixPath就是一条从treeNode(包括treeNode)到根节点(不包括根节点)的路径\n",
|
||||
"def ascendTree(leafNode, prefixPath):\n",
|
||||
" if leafNode.parent != None:\n",
|
||||
" prefixPath.append(leafNode.name)\n",
|
||||
" ascendTree(leafNode.parent, prefixPath)\n",
|
||||
"\n",
|
||||
"# 为给定元素项生成一个条件模式基(前缀路径)。basePet表示输入的频繁项,treeNode为当前FP树中对应的第一个节点\n",
|
||||
"# 函数返回值即为条件模式基condPats,用一个字典表示,键为前缀路径,值为计数值。\n",
|
||||
"def findPrefixPath(basePat, treeNode):\n",
|
||||
" condPats = {} # 存储条件模式基\n",
|
||||
" while treeNode != None:\n",
|
||||
" prefixPath = [] # 用于存储前缀路径\n",
|
||||
" ascendTree(treeNode, prefixPath) # 生成前缀路径\n",
|
||||
" if len(prefixPath) > 1:\n",
|
||||
" condPats[frozenset(prefixPath[1:])] = treeNode.count # 出现的数量就是当前叶子节点的数量\n",
|
||||
" treeNode = treeNode.nodeLink # 遍历下一个相同元素\n",
|
||||
" return condPats\n",
|
||||
"\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": 4,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"# =================================================递归查找频繁项集===============================================\n",
|
||||
"# 根据事务集获取FP树和频繁项。\n",
|
||||
"# 遍历频繁项,生成每个频繁项的条件FP树和条件FP树的频繁项\n",
|
||||
"# 这样每个频繁项与他条件FP树的频繁项都构成了频繁项集\n",
|
||||
"\n",
|
||||
"# inTree和headerTable是由createTree()函数生成的事务集的FP树。\n",
|
||||
"# minSup表示最小支持度。\n",
|
||||
"# preFix请传入一个空集合(set([])),将在函数中用于保存当前前缀。\n",
|
||||
"# freqItemList请传入一个空列表([]),将用来储存生成的频繁项集。\n",
|
||||
"def mineTree(inTree, headerTable, minSup, preFix, freqItemList):\n",
|
||||
" # 对频繁项按出现的数量进行排序进行排序\n",
|
||||
" sorted_headerTable = sorted(headerTable.items(), key=lambda p: p[1][0]) #返回重新排序的列表。每个元素是一个元组,[(key,[num,treeNode],())\n",
|
||||
" bigL = [v[0] for v in sorted_headerTable] # 获取频繁项\n",
|
||||
" for basePat in bigL:\n",
|
||||
" newFreqSet = preFix.copy() # 新的频繁项集\n",
|
||||
" newFreqSet.add(basePat) # 当前前缀添加一个新元素\n",
|
||||
" freqItemList.append(newFreqSet) # 所有的频繁项集列表\n",
|
||||
" condPattBases = findPrefixPath(basePat, headerTable[basePat][1]) # 获取条件模式基。就是basePat元素的所有前缀路径。它像一个新的事务集\n",
|
||||
" myCondTree, myHead = createTree(condPattBases, minSup) # 创建条件FP树\n",
|
||||
"\n",
|
||||
" if myHead != None:\n",
|
||||
" # 用于测试\n",
|
||||
" print('conditional tree for:', newFreqSet)\n",
|
||||
" myCondTree.disp()\n",
|
||||
" mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList) # 递归直到不再有元素\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": 5,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"# 生成数据集\n",
|
||||
"def loadSimpDat():\n",
|
||||
" simpDat = [['r', 'z', 'h', 'j', 'p'],\n",
|
||||
" ['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],\n",
|
||||
" ['z'],\n",
|
||||
" ['r', 'x', 'n', 'o', 's'],\n",
|
||||
" ['y', 'r', 'x', 'z', 'q', 't', 'p'],\n",
|
||||
" ['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]\n",
|
||||
" return simpDat"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": 6,
|
||||
"metadata": {},
|
||||
"outputs": [
|
||||
{
|
||||
"name": "stdout",
|
||||
"output_type": "stream",
|
||||
"text": [
|
||||
"conditional tree for: {'y'}\n",
|
||||
" Null Set 1\n",
|
||||
" x 3\n",
|
||||
" z 3\n",
|
||||
"conditional tree for: {'y', 'z'}\n",
|
||||
" Null Set 1\n",
|
||||
" x 3\n",
|
||||
"conditional tree for: {'t'}\n",
|
||||
" Null Set 1\n",
|
||||
" y 3\n",
|
||||
" x 3\n",
|
||||
" z 3\n",
|
||||
"conditional tree for: {'x', 't'}\n",
|
||||
" Null Set 1\n",
|
||||
" y 3\n",
|
||||
"conditional tree for: {'z', 't'}\n",
|
||||
" Null Set 1\n",
|
||||
" y 3\n",
|
||||
" x 3\n",
|
||||
"conditional tree for: {'z', 'x', 't'}\n",
|
||||
" Null Set 1\n",
|
||||
" y 3\n",
|
||||
"conditional tree for: {'s'}\n",
|
||||
" Null Set 1\n",
|
||||
" x 3\n",
|
||||
"conditional tree for: {'x'}\n",
|
||||
" Null Set 1\n",
|
||||
" z 3\n",
|
||||
"[{'r'}, {'y'}, {'y', 'x'}, {'y', 'z'}, {'y', 'x', 'z'}, {'t'}, {'y', 't'}, {'x', 't'}, {'y', 'x', 't'}, {'z', 't'}, {'y', 'z', 't'}, {'z', 'x', 't'}, {'y', 'z', 'x', 't'}, {'s'}, {'x', 's'}, {'x'}, {'x', 'z'}, {'z'}]\n"
|
||||
]
|
||||
}
|
||||
],
|
||||
"source": [
|
||||
"# 将数据集转化为目标格式\n",
|
||||
"def createInitSet(dataSet):\n",
|
||||
" retDict = {}\n",
|
||||
" for trans in dataSet:\n",
|
||||
" retDict[frozenset(trans)] = 1\n",
|
||||
" return retDict\n",
|
||||
"\n",
|
||||
"if __name__=='__main__':\n",
|
||||
" minSup =3\n",
|
||||
" simpDat = loadSimpDat() # 加载数据集\n",
|
||||
" initSet = createInitSet(simpDat) # 转化为符合格式的事务集\n",
|
||||
" myFPtree, myHeaderTab = createTree(initSet, minSup) # 形成FP树\n",
|
||||
" # myFPtree.disp() # 打印树\n",
|
||||
"\n",
|
||||
" freqItems = [] # 用于存储频繁项集\n",
|
||||
" mineTree(myFPtree, myHeaderTab, minSup, set([]), freqItems) # 获取频繁项集\n",
|
||||
" print(freqItems) # 打印频繁项集"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**FP-growth算法总结**\n",
|
||||
"\n",
|
||||
"FP-growth算法是一种用于发现数据集中频繁模式的有效方法。\n",
|
||||
"\n",
|
||||
"FP-growth算法利用Apriori原则,执行更快。Apriori算法产生候选项集,然后扫描数据集来检查它们是否频繁。\n",
|
||||
"\n",
|
||||
"由于只对数据集扫描两次,因此FP-growth算法执行更快。\n",
|
||||
"\n",
|
||||
"在FP-growth算法中,数据集存储在一个称为FP树的结构中。\n",
|
||||
"\n",
|
||||
"FP树构建完成后,可以通过查找元素项的条件基及构建条件FP树来发现频繁项集。\n",
|
||||
"\n",
|
||||
"该过程不断以更多元素作为条件重复进行,直到FP树只包含一个元素为止。\n",
|
||||
"\n",
|
||||
"优缺点:\n",
|
||||
"\n",
|
||||
" - 优点:一般要快于Apriori。 \n",
|
||||
" - 缺点:实现比较困难,在某些数据集上性能会下降。 \n",
|
||||
" - 适用数据类型:离散型数据。"
|
||||
]
|
||||
}
|
||||
],
|
||||
"metadata": {
|
||||
"kernelspec": {
|
||||
"display_name": "Python 3",
|
||||
"language": "python",
|
||||
"name": "python3"
|
||||
},
|
||||
"language_info": {
|
||||
"codemirror_mode": {
|
||||
"name": "ipython",
|
||||
"version": 3
|
||||
},
|
||||
"file_extension": ".py",
|
||||
"mimetype": "text/x-python",
|
||||
"name": "python",
|
||||
"nbconvert_exporter": "python",
|
||||
"pygments_lexer": "ipython3",
|
||||
"version": "3.6.9"
|
||||
}
|
||||
},
|
||||
"nbformat": 4,
|
||||
"nbformat_minor": 4
|
||||
}
|
||||
255
aihub/machine-learning/基于规则的分类器(1).ipynb
Normal file
255
aihub/machine-learning/基于规则的分类器(1).ipynb
Normal file
@ -0,0 +1,255 @@
|
||||
{
|
||||
"cells": [
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 算法简介\n",
|
||||
"\n",
|
||||
"基于规则的分类器是**使用一组\"if...then...\"规则来对记录进行分类的技术。**\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"模型的规则用 $R =(r_1 ∨ r_2 ∨ ••• ∨ r_k)$表示"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
">n其中R称作规则集,$r_i$ 是分类规则。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"每一个分类规则可以表示为如下形式:"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
">n$r_i:(条件i)→y_i$"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"规则右边称为**规则后件,包含预测类$y_i$。** 规则左边称为**规则前件或前提。**\n",
|
||||
"\n",
|
||||
"它是**属性和属性值的合取**:$条件i=(A_1\\, op \\,\\, v_1)∧(A_2\\, op \\,\\, v_2)∧•••∧(A_n \\, op\\,\\, v_n)$"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"其中$(A_j,v_j)$是属性-值对,op是比较运算符,取自集合${=,≠,﹤,﹥,≤,≥}$。\n",
|
||||
"\n",
|
||||
"每一个属性和属性值$(A_j \\, \\, op\\, \\, v_j)$称为一个合取项。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"如果规则$r$的前件和记录$x$的属性匹配,则称**$r$覆盖$x$**。\n",
|
||||
"\n",
|
||||
"当$r$覆盖给定的记录时,称**$r$被触发**。当所有规则中只有规则$r$被触发,则称**$r$被激活**。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"分类规则的质量可以用**覆盖率(coverage)和准确率(accuracy)**来度量。\n",
|
||||
"\n",
|
||||
"给定数据集D和分类规则 $r:A→y$,规则的覆盖率定义为**D中触发规则r的记录所占的比例。**\n",
|
||||
"\n",
|
||||
"准确率或置信因子定义为**触发$r$的记录中类标号等于$y$的记录所占的比例。**"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"$Coverage(r)= |A| / |D|$\n",
|
||||
"\n",
|
||||
"$Accuracy(r)= |A∩y| / |A|$\n",
|
||||
"\n",
|
||||
"其中$|A|$是**满足规则前件的记录数**,$|A∩y|$是**同时满足规则前件和后件的记录数,D是记录总数。**"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 工作原理"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"### 基于规则的分类器所产生的规则集的两个重要性质:\n",
|
||||
"\n",
|
||||
">互斥规则:如果规则集R中不存在两条规则被同一条记录触发,则称规则集R中的规则是互斥的。这个性质确保每条记录至多被R中的一条规则覆盖。\n",
|
||||
"\n",
|
||||
">穷举规则:如果对属性值的任意组合,R中都存在一条规则加以覆盖,则称规则集R具有穷举覆盖。这个性质确保每一条记录都至少被R中的一条规则覆盖。\n",
|
||||
"\n",
|
||||
"**这两个性质共同作用,保证每一条记录被且仅被一条规则覆盖。**\n",
|
||||
"\n",
|
||||
"如果规则集**不是穷举的**,那么必须添加一个默认规则 $r_d:() → y_d$来覆盖那些未被覆盖的记录。\n",
|
||||
"\n",
|
||||
"默认规则的前件为空,当所有其他规则失效时触发。$y_d$是默认类,通常被指定为没有被现存规则覆盖的训练记录的多数类。\n",
|
||||
"\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"如果规则集**不是互斥的**,那么一条记录可能被多条规则覆盖,这些规则的预测可能会相互冲突,解决这个问题有如下两种方法:\n",
|
||||
"\n",
|
||||
">1、有序规则:规则集中的规则按照优先级降序排列,优先级的定义有多种方法(如基于准确率、覆盖率、总描述长度或规则产生的顺序等)。\n",
|
||||
"\n",
|
||||
">有序规则的规则集也称为决策表。当测试记录出现时,由覆盖记录的最高秩的规则对其进行分类,这就避免由多条分类规则来预测而产生的类冲突的问题。\n",
|
||||
"\n",
|
||||
">2、无序规则:允许一条测试记录触发多条分类规则,把每条被触发规则的后件看作是对相应类的一次投票,然后计票确定测试记录的类标号。\n",
|
||||
"\n",
|
||||
">通常把记录指派到得票最多的类。\n",
|
||||
"\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"本文重点讨论**使用有序规则的基于规则的分类器。**"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 如果被触发的多个规则指向不同的类"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"解决这个问题的核心思想,就是需要对不同规则进行优先级排序,取优先级高的规则所对应的类别作为元组的分类。 "
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"两种解决方案: "
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"\n",
|
||||
"**规模序**:把最高优先级权赋予具有“最苛刻”要求的被触发的规则,其中苛刻性用规则前件的规模度量。也就是说,激活具有最多属性测试的被触发的规则。\n",
|
||||
"\n",
|
||||
"**规则序**:指预先确定规则的优先次序。这种序的确定可以基于两种方法:基于类的序和基于规则的序 "
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 规则的排序方案"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"对规则的排序可以逐条规则进行或者逐个类进行。\n",
|
||||
"\n",
|
||||
"**基于规则质量的排序方案**:这个方案依据规则质量的某种度量对规则进行排序。这种排序方案确保每一个测试记录都是由覆盖它的“最好的”规则来分类。这种规则的质量可以是准确度、覆盖率或规模等。该方案的潜在缺点是**规则的秩(规则合取项的个数)越低越难解释,因为每个规则都假设所有排在它前面的规则不成立。**\n",
|
||||
"\n",
|
||||
"**基于类标号的排序方案**:根据类的重要性来对规则进行排序。即最重要的类对应的规则先出现,次重要的类对应的规则紧接着出现,以此类推。对于类的重要性的衡量标准有很多,比如类的普遍性、误分类代价等。这使得规则的解释稍微容易一些。在这种方案中,属于同一个分类的规则在规则集R中一起出现。然后,这些规则根据它们所属的分类信息一起排序。同一个分类的规则之间的相对顺序并不重要,只要其中一个规则被激发,类标号就会赋给测试记录。然而,质量较差的规则可能碰巧预测较高秩的类,从而导致高质量的规则被忽略。\n",
|
||||
"\n",
|
||||
"大部分基于规则的分类器(如CS4.5规则和RIPPER)都采用**基于类标号的排序方案。**"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 如何建立基于规则的分类器"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"为了建立基于规则的分类器,需要提取一组规则来识别数据集的属性和类标号之间的关键联系。提取分类规则的方法有两大类:\n",
|
||||
"\n",
|
||||
">(1)直接方法,直接从数据中提取分类规则;\n",
|
||||
"\n",
|
||||
">(2)间接方法,从其他分类模型(如决策树和神经网络)中提取分类规则。\n",
|
||||
"\n",
|
||||
"直接方法把属性空间分为较小的子空间,以便于属于一个子空间的所有记录可以使用一个分类规则进行分类。\n",
|
||||
"\n",
|
||||
"间接方法使用分类规则为较复杂的分类模型提供简洁的描述。\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 规则提取的直接方法"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"顺序覆盖:算法经常被用来从直接数据中提取规则,规则基于某种评估度量以**贪心**的方式增长。\n",
|
||||
"\n",
|
||||
"该算法从包含多个类的数据集中一次提取一个类的规则。决定哪一个类的规则最先产生的标准取决于多种因素,如类的普遍性(即训练记录中属于特定类的记录的比例),或者给定类中误分类记录的代价。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": []
|
||||
}
|
||||
],
|
||||
"metadata": {
|
||||
"kernelspec": {
|
||||
"display_name": "Python 3",
|
||||
"language": "python",
|
||||
"name": "python3"
|
||||
},
|
||||
"language_info": {
|
||||
"codemirror_mode": {
|
||||
"name": "ipython",
|
||||
"version": 3
|
||||
},
|
||||
"file_extension": ".py",
|
||||
"mimetype": "text/x-python",
|
||||
"name": "python",
|
||||
"nbconvert_exporter": "python",
|
||||
"pygments_lexer": "ipython3",
|
||||
"version": "3.6.9"
|
||||
}
|
||||
},
|
||||
"nbformat": 4,
|
||||
"nbformat_minor": 4
|
||||
}
|
||||
301
aihub/machine-learning/基于规则的分类器(2).ipynb
Normal file
301
aihub/machine-learning/基于规则的分类器(2).ipynb
Normal file
@ -0,0 +1,301 @@
|
||||
{
|
||||
"cells": [
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 1. Learn-One-Rule函数"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"Learn-One-Rule函数的目标是**提取一个分类规则,该规则覆盖训练集中的大量正例,没有或仅覆盖少量反例。**\n",
|
||||
"\n",
|
||||
"然而,由于搜索空间呈指数大小,要找到一个最佳的规则的计算开销很大。\n",
|
||||
"\n",
|
||||
"Learn-One-Rule函数通过以一种贪心的方式的增长规则来解决指数搜索问题。\n",
|
||||
"\n",
|
||||
"它产生一个初始规则$r$,并不断对该规则求精,直到满足某种终止条件为止。然后修剪该规则,以改进它的泛化误差。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**规则增长策略**:\n",
|
||||
"\n",
|
||||
"常见的分类规则增长策略有两种:\n",
|
||||
"\n",
|
||||
"从**一般到特殊**和**从特殊到一般。**\n",
|
||||
"\n",
|
||||
">在从一般到特殊的策略中,先建立一个初始规则$r:\\{\\}→y$,其中左边是一个空集,右边包含目标类。\n",
|
||||
"\n",
|
||||
"该规则的质量很差,因为它覆盖训练集中的所有样例。接着加入新的合取项来提高规则的质量,直到满足终止条件为止(例如,加入的合取项已不能提高规则的质量)。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
">对于从特殊到一般的策略,可以随机地选择一个正例作为规则增长的初始种子。\n",
|
||||
"\n",
|
||||
"再求精步,通过删除规则的一个合取项,使其覆盖更多的正例来范化规则。重复求精步,直到满足终止条件为止(例如,当规则开始覆盖反例时为止)。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"由于规则的贪心的方式增长,以上方法可能会产生次优规则。\n",
|
||||
"\n",
|
||||
"为了避免这种问题,可以采用束状搜索(beam search)。\n",
|
||||
"\n",
|
||||
"算法维护$k$个最佳候选规则,各候选规则各自在其前件中添加或删除合取项而独立地增长。\n",
|
||||
"\n",
|
||||
"评估候选规则的质量,选出$k$个最佳候选进入下一轮迭代。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**规则评估:**\n",
|
||||
"\n",
|
||||
"在规则的增长过程中,**需要一种评估度量来确定应该添加(或删除)哪个合取项**。\n",
|
||||
"\n",
|
||||
"准确率就是一个很明显的选择,因为它明确地给出了被规则正确分类的训练样例的比例。**然而把准确率作为标准的一个潜在的局限性是它没有考虑规则的覆盖率。**"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"下面的方法可以用来处理该问题:"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"(1)**可以使用统计检验剪除覆盖率较低的规则。**\n",
|
||||
"\n",
|
||||
"例如,我们可以计算下面的似然比(likelihood ratio)统计量:\n",
|
||||
"\n",
|
||||
"$$R=2\\sum_{i=1}^mf_ilog(\\frac{f_i}{e_i})$$\n",
|
||||
"\n",
|
||||
"其中,$m$是类的个数,$f_i$ 是被规则覆盖的类$i$的样本的观测频率,$e_i$ 是规则作随机猜想的期望频率。注意R是满足自由度为$m-1$的$χ^2$分布。较大的R值说明该规则做出的正确预测数显著地大于随机猜测的结果。\n",
|
||||
"\n",
|
||||
"(2)**可以使用一种考虑规则覆盖率的评估度量。**\n",
|
||||
"\n",
|
||||
"考虑如下评估度量:\n",
|
||||
"$$Laplace = \\frac{f_++1}{n+k}$$\n",
|
||||
"\n",
|
||||
"$$m估计=\\frac{f_++kp_+}{n+k}$$\n",
|
||||
"\n",
|
||||
"其中n是规则覆盖的样例数,f+是规则覆盖的正例数,k是类的总数,p+是正类的先验概率。注意当p+=1/k时,m估计等价于Laplace度量。\n",
|
||||
"\n",
|
||||
"(3)**另一种可以使用的评估度量是考虑规则的支持度计数的评估度量。**\n",
|
||||
"\n",
|
||||
"FOIL信息增益就是一种这样的度量。规则的支持度计数对应于它所覆盖的正例数。\n",
|
||||
"\n",
|
||||
"假设规则$r : A→+$覆盖$p_0$个正例和$n_0$个反例。增加新的合取项B,扩展后的规则$r' : A∧B→+$覆盖$p_1$个正例和$n_1$个反例。\n",
|
||||
"\n",
|
||||
"根据以上信息,扩展后规则的FOIL信息增益定义为:\n",
|
||||
"\n",
|
||||
"$$FOIL信息增益=p_1*(log_2\\frac{p_1}{p_1+n_1}-log_2\\frac{p_0}{p_0+n_0})$$\n",
|
||||
"\n",
|
||||
"由于该度量与$p1$和$p1/p1+n1$成正比,因此它更倾向于选择那些高支持度计数和高准确率的规则。\n",
|
||||
"\n",
|
||||
"规则减枝 \n",
|
||||
"\n",
|
||||
"可以对Learn-One-Rule函数产生的规则进行减枝,以改善它们的泛化误差。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 2. 顺序覆盖基本原理\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"规则提取出来后,顺序覆盖算法必须删除该规则所覆盖的所有正例和反例。\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 3. RIPPER算法"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"为了阐明规则提取的直接方法,考虑一种广泛使用的规则归纳算法,叫作RIPPER算法。\n",
|
||||
"\n",
|
||||
"该算法的复杂度几乎线性地随训练样例的数目增长,并且特别适合为类分布不平衡的数据集建立模型。\n",
|
||||
"\n",
|
||||
"RIPPER也能很好地处理噪声数据集,因为它使用一个确认数据集来防止模型过分拟合。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"对两类问题,RIPPER算法选择以多数类作为默认类,并为预测少数类学习规则。\n",
|
||||
"\n",
|
||||
"对于多类问题,先按类的频率对类进行排序,设$(y1,y2,…,yc)$是排序后的类,其中$y_1$是最不频繁的类,$y_c$是最频繁的类。\n",
|
||||
"\n",
|
||||
"第一次迭代中,把属于$y_1$的样例标记为正例,而把其他类的样例标记为反例,使用顺序覆盖算法产生区分正例和反例的规则。\n",
|
||||
"\n",
|
||||
"接下来,RIPPER提取区分$y_2$和其他类的规则。重复该过程,直到剩下类$y_c$,此时$y_c$作为默认类。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**规则增长**\n",
|
||||
"\n",
|
||||
"RIPPER算法使用从一般到特殊的策略进行规则增长,使用FOIL信息增益来选择最佳合取项添加到规则前件中。\n",
|
||||
"\n",
|
||||
"当规则开始覆盖反例时,停止添加合取项。\n",
|
||||
"\n",
|
||||
"新规则根据其在确认集上的性能进行减枝。\n",
|
||||
"\n",
|
||||
"计算下面的度量来确定规则是否需要减枝:$(p-n)/(p+n)$,其中p和n分别是被规则覆盖的确认集中的正例和反例数目,关于规则在确认集上的准确率,该度量是单调的。\n",
|
||||
"\n",
|
||||
"如果减枝后该度量增加,那么就去掉该合取项。减枝是从最后添加的合取项开始的。\n",
|
||||
"\n",
|
||||
"例如给定规则$ABCD→y$,RIPPER算法先检查D是否应该减枝,然后是CD、BCD等。\n",
|
||||
"\n",
|
||||
"尽管原来的规则仅覆盖正例,但是减枝后的规则可能会覆盖训练集中的一些反例。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**建立规则集** \n",
|
||||
"\n",
|
||||
"规则生成后,它所覆盖的所有正例和反例都要被删除。只要该规则不违反基于最小描述长度的终止条件,就把它添加到规则集中。\n",
|
||||
"\n",
|
||||
"如果新规则把规则集的总描述长度增加了至少d个比特位,那么RIPPER就停止把该规则加入到规则集(默认的d是64位)。\n",
|
||||
"\n",
|
||||
"RIPPER使用的另一个终止条件是规则在确认集上的错误率不超过50%。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"RIPPER算法也采用其他的优化步骤来决定规则集中现存的某些规则能否被更好的规则替代。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 规则提取的间接方法"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"原则上,决策树从根节点到叶节点的每一条路径都可以表示为一个分类规则。\n",
|
||||
"\n",
|
||||
"路径中的测试条件构成规则前件的合取项,叶节点的类标号赋给规则后件。\n",
|
||||
"\n",
|
||||
"注意,规则集是完全的,包含的规则是互斥的。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"下面,介绍C4.5规则算法所采用的从决策树生成规则集的方法。\n",
|
||||
"\n",
|
||||
"**规则产生**\n",
|
||||
"\n",
|
||||
"决策树中从根节点到叶节点的每一条路径都产生一条分类规则。\n",
|
||||
"\n",
|
||||
"给定一个分类规则$r : A→y$,考虑简化后的规则 $r': A' →y$,其中A'是从A去掉一个合取项后得到的。\n",
|
||||
"\n",
|
||||
"只要简化后的规则的误差率低于原规则的误差率,就保留其中悲观误差率最低的规则。\n",
|
||||
"\n",
|
||||
"重复规则减枝步骤,直到规则的悲观误差不能再改进为止。由于某些规则在减枝后会变得相同,因此必须丢弃重复规则。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**规则排序** \n",
|
||||
"\n",
|
||||
"产生规则集后,C4.5规则算法使用基于类的排序方案对提取的规则定序。\n",
|
||||
"\n",
|
||||
"预测同一个类的规则分到同一个子集中。计算每个子集的总描述长度,然后各类按照总描述长度由小到大排序。\n",
|
||||
"\n",
|
||||
"具有最小描述长度的类优先级最高,因为期望它包含最好的规则集。类的总描述长度等于Lexception+g×Lmodel,其中Lexception是对误分类样例编码所需的比特位数,Lmodel是对模型编码所需要的比特位数,而g是调节参数,默认值为0.5,。\n",
|
||||
"\n",
|
||||
"调节参数的值取决于模型中冗余属性的数量,如果模型含有很多冗余属性,那么调节参数的值会很小。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 基于规则的分类器的特征"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"基于规则的分类器有如下特点:\n",
|
||||
"\n",
|
||||
">规则集的表达能力几乎等价于决策树,因为决策树可以用互斥和穷举的规则集表示。\n",
|
||||
"\n",
|
||||
">基于规则分类器和决策树分类器都对属性空间进行直线划分,并将类指派到每个划分。\n",
|
||||
"\n",
|
||||
">然而,如果基于规则的分类器允许一条记录触发多条规则的话,就可以构造一个更加复杂的决策边界。\n",
|
||||
"\n",
|
||||
">基于规则的分类器通常被用来产生更易于解释的描述性模型,而模型的性能却可与决策树分类器相媲美。\n",
|
||||
"\n",
|
||||
">被很多基于规则的分类器(如RIPPER)所采用的基于类的规则定序方法非常适于处理类分布不平衡的数据集。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": []
|
||||
}
|
||||
],
|
||||
"metadata": {
|
||||
"kernelspec": {
|
||||
"display_name": "Python 3",
|
||||
"language": "python",
|
||||
"name": "python3"
|
||||
},
|
||||
"language_info": {
|
||||
"codemirror_mode": {
|
||||
"name": "ipython",
|
||||
"version": 3
|
||||
},
|
||||
"file_extension": ".py",
|
||||
"mimetype": "text/x-python",
|
||||
"name": "python",
|
||||
"nbconvert_exporter": "python",
|
||||
"pygments_lexer": "ipython3",
|
||||
"version": "3.6.9"
|
||||
}
|
||||
},
|
||||
"nbformat": 4,
|
||||
"nbformat_minor": 4
|
||||
}
|
||||
@ -86,7 +86,35 @@
|
||||
"\n",
|
||||
"每行为一个文档(链接或者文档名),每列为一个文档特征(单词),每个单元格的取值为单词在文档中出现的次数。\n",
|
||||
"\n",
|
||||
"[数据集点击下载](http://luanpeng.oss-cn-qingdao.aliyuncs.com/csdn/python/%E8%81%9A%E7%B1%BB/blogdata.txt)\n"
|
||||
"\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": 37,
|
||||
"metadata": {},
|
||||
"outputs": [
|
||||
{
|
||||
"name": "stdout",
|
||||
"output_type": "stream",
|
||||
"text": [
|
||||
"--2022-09-17 10:41:39-- http://luanpeng.oss-cn-qingdao.aliyuncs.com/csdn/python/%E8%81%9A%E7%B1%BB/blogdata.txt\n",
|
||||
"Resolving luanpeng.oss-cn-qingdao.aliyuncs.com (luanpeng.oss-cn-qingdao.aliyuncs.com)... 47.104.37.237\n",
|
||||
"Connecting to luanpeng.oss-cn-qingdao.aliyuncs.com (luanpeng.oss-cn-qingdao.aliyuncs.com)|47.104.37.237|:80... connected.\n",
|
||||
"HTTP request sent, awaiting response... 200 OK\n",
|
||||
"Length: 147123 (144K) [text/plain]\n",
|
||||
"Saving to: ‘blogdata.txt.2’\n",
|
||||
"\n",
|
||||
"blogdata.txt.2 100%[===================>] 143.67K --.-KB/s in 0.06s \n",
|
||||
"\n",
|
||||
"2022-09-17 10:41:39 (2.29 MB/s) - ‘blogdata.txt.2’ saved [147123/147123]\n",
|
||||
"\n"
|
||||
]
|
||||
}
|
||||
],
|
||||
"source": [
|
||||
"# 数据集下载\n",
|
||||
"!wget http://luanpeng.oss-cn-qingdao.aliyuncs.com/csdn/python/%E8%81%9A%E7%B1%BB/blogdata.txt"
|
||||
]
|
||||
},
|
||||
{
|
||||
@ -114,7 +142,7 @@
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"execution_count": 38,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
@ -166,7 +194,7 @@
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"execution_count": 39,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
@ -201,7 +229,7 @@
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"execution_count": 40,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
@ -239,7 +267,7 @@
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"execution_count": 41,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
@ -298,7 +326,7 @@
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": 3,
|
||||
"execution_count": 42,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
@ -319,7 +347,7 @@
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"execution_count": 43,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
@ -340,7 +368,7 @@
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"execution_count": 44,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
@ -378,7 +406,7 @@
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"execution_count": 45,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
@ -412,11 +440,13 @@
|
||||
},
|
||||
{
|
||||
"cell_type": "code",
|
||||
"execution_count": null,
|
||||
"execution_count": 48,
|
||||
"metadata": {},
|
||||
"outputs": [],
|
||||
"source": [
|
||||
"if __name__=='__main__':\n",
|
||||
" from math import sqrt #导库\n",
|
||||
" from PIL import Image,ImageDraw #导库\n",
|
||||
" blognames,words,data = readfile('blogdata.txt') #加载数据集\n",
|
||||
" clust = hcluster(data) #构建聚类树\n",
|
||||
" drawdendrogram(clust,blognames,jpeg='blogclust.jpg') # 绘制聚类树"
|
||||
|
||||
335
aihub/machine-learning/极大似然估计、EM算法.ipynb
Normal file
335
aihub/machine-learning/极大似然估计、EM算法.ipynb
Normal file
@ -0,0 +1,335 @@
|
||||
{
|
||||
"cells": [
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 极大似然"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"极大似然(Maximum Likelihood)估计为用于已知模型的**参数估计**的统计学方法。\n",
|
||||
"\n",
|
||||
"也就是求使得似然函数最大的代估参数的值。而**似然函数就是如果参数已知则已出现样本出现的概率**。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"比如,我们想了解抛硬币是正面(head)的概率分布$θ$;那么可以通过最大似然估计方法求得:\n",
|
||||
"\n",
|
||||
"$$\\hat{θ} =argmax_x l(θ)=argmax_x θ^8 (1−θ)^2 $$\n",
|
||||
"\n",
|
||||
"其中,$l(θ)$为观测变量序列的似然函数。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"所以最大似然方法估计参数,就是先假设参数已知,然后用参数,求出样本出现的概率。如果是多个样本,就是多个样本的联合概率最大"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"求解使似然函数最大的代估参数,常规的做法就是对似然函数求导,求使导数为0的自变量的值,以及左右边界线的值。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"例如:\n",
|
||||
"\n",
|
||||
"对$l(θ)$求偏导\n",
|
||||
"\n",
|
||||
"$$\\frac{∂l(θ)}{∂θ} =θ^7 (1−θ)(8−10θ)⇒\\hat{θ} =0.8 $$\n",
|
||||
"\n",
|
||||
"但是如果似然函数不是凹函数(concave),求解极大值困难。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"一般地,使用与之具有相同单调性的log-likelihood,如图所示也就是将似然函数求log。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"\n",
|
||||
"\n",
|
||||
"所谓的凹函数和凸函数,凹函数斜率逐渐减小,凸函数斜率逐渐增大。\n",
|
||||
"\n",
|
||||
"所以凹函数“容易”求解极大值(极值为0时),凸函数“容易”求解极小值(极值为0时)。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# EM算法"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"EM算法(Expectation Maximization)是在含有隐变量(latent variable)的模型下计算最大似然的一种算法。\n",
|
||||
"\n",
|
||||
"所谓隐变量,是指**我们没有办法观测到的变量。**\n",
|
||||
"\n",
|
||||
"比如,有两枚硬币A、B,每一次随机取一枚进行抛掷,我们只能观测到硬币的正面与反面,而不能观测到每一次取的硬币是否为A;则称每一次的选择抛掷硬币为隐变量。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"用Y表示观测数据,Z表示隐变量;\n",
|
||||
"\n",
|
||||
"Y和Z连在一起称为完全数据( complete-data ),观测数据Y又称为不完全数据(incomplete-data)。\n",
|
||||
"\n",
|
||||
"观测数据的似然函数:\n",
|
||||
"$$P(Y|θ)=∑ _z P(Z|θ)P(Y|Z,θ) $$"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"求模型参数的极大似然估计:\n",
|
||||
"\n",
|
||||
"$$\\hat{θ} =argmax_{θ} logP(Y|θ) $$"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"因为含有隐变量,此问题无法求解。因此,Dempster等人提出EM算法用于迭代求解近似解。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"所以EM算法是一种特殊情况下的最大似然求解方法。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"EM算法比较简单,分为两个步骤:"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
" - E步(E-step),以当前参数$θ^{(i)}$ 计算$Z$的期望值。因为期望值中不再包含未知的隐含变量Z,所以是可以计算的。\n",
|
||||
"\n",
|
||||
"$$Q(θ,θ^{(i)} )=E_Z [logP(Y,X|θ)|Y,θ^{(i)} ] $$\n",
|
||||
"\n",
|
||||
" - M步(M-step),求使$Q(θ,θ^{(i)})$极大化的$θ$,确定第$i+1$次迭代的参数的估计值$θ^{(i+1)}$\n",
|
||||
"\n",
|
||||
"$$θ^{(i+1)} =argmax_θ Q(θ,θ^{(i)} ) $$"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"如此迭代直至算法收敛。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 案例"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"如图所示,有两枚硬币A、B,每一个实验随机取一枚抛掷10次,共5个实验,我们可以观测到每一次所取的硬币,估计参数A、B为正面的概率$θ=(θ_A ,θ_B )$ ,根据极大似然估计求解。\n",
|
||||
"\n",
|
||||
""
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"如果我们不能观测到每一次所取的硬币,只能用EM算法估计模型参数,算法流程如图所示:\n",
|
||||
"\n",
|
||||
""
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"隐变量$Z$为每次实验中选择A或B的概率,并初始化A为正面的概率为0.6,B为正面的概率为0.5。\n",
|
||||
"\n",
|
||||
"实验进行了5次。每次都要进行一遍EM操作。每次都要计算隐含变量。取A的概率,和取B的概率。\n",
|
||||
"\n",
|
||||
"然后更新代估参数$θ_A$(A为正面的概率)和$θ_B$(B为正面的概率)的值。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"在初始化$θ_A=0.6$和$θ_B=0.5$后第一次实验后计算隐含变量(选择A的概率)为"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"$$P(z_1 =A|y_1 ,θ^0)=\\frac{z_1为A的话,样本结果出现的概率}{z_1为任何可取值的话,样本结果出现的概率}=\\frac{P(z_1 =A|y_1 ,θ^0)} { P(z_1 =A|y_1 ,θ^0)+P(z_1 =B|y_1 ,θ^0) }=\\frac{0.6^5 ∗0.4^5}{0.6^5 ∗0.4^5 +0.5^{10}} =0.45 $$"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"按照上面的计算方法可依次求出其他隐含变量$Z$,然后计算极大化的$θ^{(i)}$。\n",
|
||||
"\n",
|
||||
"经过10次迭代,最终收敛。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# K均值聚类和EM算法"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"K均值聚类是无监督的聚类算法。\n",
|
||||
"\n",
|
||||
"关于k均值聚类不了解的可以参考:https://blog.csdn.net/luanpeng825485697/article/details/78993977"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"k均值聚类的目的就是为了使下面的损失函数最小"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"$$J(c,u)=\\sum_{i=1}^m||x_i-u_{c_i}||$$\n",
|
||||
"\n",
|
||||
"其中m为样本个数,$x_i$表示第$i$个样本,$c_i$表示第i个样本所属的聚类,$u_{c_i}$表示第i个样本所属的聚类的质心。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"假设当前$J$没有达到最小值,那么首先可以固定每个类的质心$u_j$,调整每个样例的所属的类别$c_j$来让$J$函数减少,同样,固定$c_j$,调整每个类的质心$u_j$也可以使$J$减小。\n",
|
||||
"\n",
|
||||
"这两个过程就是内循环中使$J$单调递减的过程。当$J$递减到最小时,$u$和$c$也同时收敛。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**K-means与EM的关系**"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"首先回到初始问题,我们目的是将样本分成K个类,其实说白了就是求一个样本的隐含类别y,然后利用隐含类别将x归类。\n",
|
||||
"\n",
|
||||
"由于我们事先不知道类别y,那么我们首先可以对每个样例假定一个y吧,但是怎么知道假定的对不对呢?怎样评价假定的好不好呢?"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"我们使用样本的极大似然估计来度量,这里就是x和y的联合分布P(x,y)了。\n",
|
||||
"\n",
|
||||
"如果找到的y能够使P(x,y)最大,那么我们找到的y就是样例x的最佳类别了,x顺手就聚类了。\n",
|
||||
"\n",
|
||||
"但是我们第一次指定的y不一定会让P(x,y)最大,而且P(x,y)还依赖于其他未知参数,当然在给定y的情况下,我们可以调整其他参数让P(x,y)最大。\n",
|
||||
"\n",
|
||||
"但是调整完参数后,我们发现有更好的y可以指定,那么我们重新指定y,然后再计算P(x,y)最大时的参数,反复迭代直至没有更好的y可以指定。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**这个过程有几个难点:**\n",
|
||||
"\n",
|
||||
">第一怎么假定y?是每个样例硬指派一个y还是不同的y有不同的概率,概率如何度量。(kmean中是硬指定,距离哪个聚类近就属于哪个聚类)\n",
|
||||
"\n",
|
||||
">第二如何估计$P(x,y)$,$P(x,y)$还可能依赖很多其他参数,如何调整里面的参数让$P(x,y)$最大。($J$函数最小来代替$P(x,y)$最大,我们可以将这些参数写成$θ$,更简单的理解$θ$就是k个质心的选择)"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**按照EM算法思想:** E步就是估计隐含类别y的期望值,M步调整其他参数使得在给定类别y的情况下,极大似然估计$P(x,y)$能够达到极大值。然后在其他参数确定的情况下,重新估计y,周而复始,直至收敛。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"E步(E-step),以当前参数$θ$计算$Z$的期望值。也就是确定隐含类别变量$c$,样本所属的分类。我们固定每个类的中心,通过对每一个样本选择最近的分类,以此优化目标函数。\n",
|
||||
"\n",
|
||||
"M步(M-step),以当前$Z$的值计算使$P(x,y)$最大的$θ$。求使$J$函数最小的$u$,也就是求每个聚类的质心。重新更新每个类的中心点,该步骤可以通过对目标函数求导实现求解$θ$,最终可得新的类中心就是类中样本的均值。\n",
|
||||
"\n",
|
||||
"这里的隐含类别变量指定方法比较特殊,属于硬指定,从k个类别中硬选出一个给样例(距离哪个聚类近就属于哪个聚类),而不是对每个类别赋予不同的概率。"
|
||||
]
|
||||
}
|
||||
],
|
||||
"metadata": {
|
||||
"kernelspec": {
|
||||
"display_name": "Python 3",
|
||||
"language": "python",
|
||||
"name": "python3"
|
||||
},
|
||||
"language_info": {
|
||||
"codemirror_mode": {
|
||||
"name": "ipython",
|
||||
"version": 3
|
||||
},
|
||||
"file_extension": ".py",
|
||||
"mimetype": "text/x-python",
|
||||
"name": "python",
|
||||
"nbconvert_exporter": "python",
|
||||
"pygments_lexer": "ipython3",
|
||||
"version": "3.6.9"
|
||||
}
|
||||
},
|
||||
"nbformat": 4,
|
||||
"nbformat_minor": 4
|
||||
}
|
||||
@ -0,0 +1,218 @@
|
||||
{
|
||||
"cells": [
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 集成学习"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**可以通过聚集多个分类器的预测结果提高分类器的分类准确率**,这一方法称为集成(Ensemble)学习或分类器组合(Classifier Combination)\n",
|
||||
"\n",
|
||||
"该方法由训练数据构建一组基分类器(Base Classifier),然后通过对每个基分类器的预测进行投票来进行分类。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"集成学习(ensemble learning)通过组合多个基分类器(base classifier)来完成学习任务,颇有点“三个臭皮匠顶个诸葛亮”的意味。\n",
|
||||
"\n",
|
||||
"基分类器一般采用的是弱可学习(weakly learnable)分类器,通过集成学习,组合成一个强可学习(strongly learnable)分类器。\n",
|
||||
"\n",
|
||||
">所谓弱可学习,是指学习的正确率仅略优于随机猜测的多项式学习算法;强可学习指正确率较高的多项式学习算法。\n",
|
||||
"\n",
|
||||
"集成学习的泛化能力一般比单一的基分类器要好,**这是因为大部分基分类器都分类错误的概率远低于单一基分类器的**。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 偏差与方差"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"“偏差-方差分解”(bias variance decomposition)是用来解释机器学习算法的泛化能力的一种重要工具。\n",
|
||||
"\n",
|
||||
"对于同一个算法,在不同训练集上学得结果可能不同。\n",
|
||||
"\n",
|
||||
"对于训练集$D={(x_1 ,y_1 ),(x_2 ,y_2 ),⋯,(x_N ,y_N )} $\n",
|
||||
"\n",
|
||||
"由于噪音,样本$x$的真实类别为$y$(在训练集中的类别为$y$),则噪声为"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"$$ξ^2 =E_D [(y_d −y)^2 ] $$"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"各种学习模型得到的预测值的期望为\n",
|
||||
"\n",
|
||||
"$$\\hat{f(x)}=E_D [f(x;D)] $$"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"使用样本数相同的不同训练集所产生的方差\n",
|
||||
"$$var(x)=E_D [(f(x;D)−\\hat{f(x)}) ^2 ] $$\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"期望输出与真实类别的差别称为bias,则\n",
|
||||
"\n",
|
||||
"$$bias^2 (x)=(\\hat{f (x)}−y)^2 $$\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# Bagging"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"Bagging(Bootstrap Aggregating)对训练数据采用自助采样(boostrap sampling),即有放回地采样数据;\n",
|
||||
"\n",
|
||||
"每一次的采样数据集训练出一个基分类器,经过M次采样得到M个基分类器,然后根据最大表决(majority vote)原则组合基分类器的分类结果。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
""
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# Boosting\n",
|
||||
"Boosting的思路则是采用重赋权(re-weighting)法迭代地训练基分类器,即对每一轮的训练数据样本赋予一个权重,并且每一轮样本的权值分布依赖上一轮的分类结果;\n",
|
||||
"\n",
|
||||
"基分类器之间采用序列式的线性加权方式进行组合。他通过迭代地训练一系列的分类器,每个分类器采用的样本分布都和上一轮的学习结果有关。其代表算法是AdaBoost, GBDT。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
""
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"从“偏差-方差分解”的角度看,Bagging关注于降低variance,而Boosting则是降低bias;\n",
|
||||
"\n",
|
||||
"Boosting的基分类器是强相关的,并不能显著降低variance。Bagging与Boosting有分属于自己流派的两大杀器:\n",
|
||||
"\n",
|
||||
"随机森林Random Forests(RF)和梯度下降树Gradient Boosting Decision Tree(GBDT)。\n",
|
||||
"\n",
|
||||
"AdaBoost属于Boosting流派。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# Bagging、Boosting二者之间的区别"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"样本选择上:\n",
|
||||
"\n",
|
||||
">Bagging:训练集是在原始集中有放回选取的,从原始集中选出的各轮训练集之间是独立的。\n",
|
||||
"\n",
|
||||
">Boosting:每一轮的训练集不变,只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。\n",
|
||||
"\n",
|
||||
"样例权重:\n",
|
||||
"\n",
|
||||
">Bagging:使用均匀取样,每个样例的权重相等。\n",
|
||||
"\n",
|
||||
">Boosting:根据错误率不断调整样例的权值,错误率越大则权重越大。\n",
|
||||
"\n",
|
||||
"预测函数:\n",
|
||||
"\n",
|
||||
">Bagging:所有预测函数的权重相等。\n",
|
||||
"\n",
|
||||
">Boosting:每个弱分类器都有相应的权重,对于分类误差小的分类器会有更大的权重。\n",
|
||||
"\n",
|
||||
"并行计算:\n",
|
||||
"\n",
|
||||
">Bagging:各个预测函数可以并行生成。\n",
|
||||
"\n",
|
||||
">Boosting:各个预测函数只能顺序生成,因为后一个模型参数需要前一轮模型的结果。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 总结"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"这两种方法都是把若干个分类器整合为一个分类器的方法,只是整合的方式不一样,最终得到不一样的效果,将不同的分类算法套入到此类算法框架中一定程度上会提高了原单一分类器的分类效果,但是也增大了计算量。\n",
|
||||
"\n",
|
||||
"**下面是将决策树与这些算法框架进行结合所得到的新的算法:**\n",
|
||||
"\n",
|
||||
">Bagging + 决策树 = 随机森林\n",
|
||||
"\n",
|
||||
">AdaBoost + 决策树 = 提升树\n",
|
||||
"\n",
|
||||
">Gradient Boosting + 决策树 = GBDT\n"
|
||||
]
|
||||
}
|
||||
],
|
||||
"metadata": {
|
||||
"kernelspec": {
|
||||
"display_name": "Python 3",
|
||||
"language": "python",
|
||||
"name": "python3"
|
||||
},
|
||||
"language_info": {
|
||||
"codemirror_mode": {
|
||||
"name": "ipython",
|
||||
"version": 3
|
||||
},
|
||||
"file_extension": ".py",
|
||||
"mimetype": "text/x-python",
|
||||
"name": "python",
|
||||
"nbconvert_exporter": "python",
|
||||
"pygments_lexer": "ipython3",
|
||||
"version": "3.6.9"
|
||||
}
|
||||
},
|
||||
"nbformat": 4,
|
||||
"nbformat_minor": 4
|
||||
}
|
||||
@ -0,0 +1,316 @@
|
||||
{
|
||||
"cells": [
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# 随机森林RF\n",
|
||||
"\n",
|
||||
"理解了bagging算法,随机森林(Random Forest,以下简称RF)就好理解了。\n",
|
||||
"\n",
|
||||
"它是Bagging算法的进化版,也就是说,它的思想仍然是bagging,但是进行了独有的改进。\n",
|
||||
"\n",
|
||||
"我们现在就来看看RF算法改进了什么。 \n",
|
||||
"\n",
|
||||
"**首先**,RF使用了CART决策树作为弱学习器。\n",
|
||||
"\n",
|
||||
"**第二**,在使用决策树的基础上,RF对决策树的建立做了改进,对于普通的决策树,我们会在节点上所有的n个样本特征中选择一个最优的特征来做决策树的左右子树划分,但是**RF通过随机选择节点上的一部分样本特征**,这个数字小于n,假设为$n_{sub}$,然后在这些随机选择的$n_{sub}$个样本特征中,选择一个最优的特征来做决策树的左右子树划分。这样进一步增强了模型的泛化能力。\n",
|
||||
"\n",
|
||||
"如果$n_{sub}=n$,则此时RF的CART决策树和普通的CART决策树没有区别。\n",
|
||||
"\n",
|
||||
"$n_{sub}$越小,则模型越健壮,当然此时对于训练集的拟合程度会变差。也就是说$n_{sub}$越小,模型的方差会减小,但是偏倚会增大。\n",
|
||||
"\n",
|
||||
"在实际案例中,一般会通过交叉验证调参获取一个合适的$n_{sub}$的值。\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"除了上面两点,RF和普通的bagging算法没有什么不同, 下面简单总结下RF的算法。\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"```\n",
|
||||
"输入为样本集$D={(x_1,y_1),(x_2,y_2),...(x_m,y_m)}$,弱分类器迭代次数T。输出为最终的强分类器$f(x)$:\n",
|
||||
"```"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"1)对于$t=1,2...,T$:\n",
|
||||
"\n",
|
||||
" - a)对训练集进行第t次随机采样,得到一个包含m个样本的采样集$D_m$\n",
|
||||
" - b)用采样集$D_m$训练第m个决策树模型$G_m(x)$,在训练决策树模型的节点的时候, 在所有的特征中选择一部分特征,在这些随机选择的部分样本特征中选择最优的特征来做决策树的左右子树划分。\n",
|
||||
"\n",
|
||||
"2) 如果是分类算法预测,则T个弱学习器投出最多票数的类别或者类别之一为最终类别。如果是回归算法,T个弱学习器得到的回归结果进行算术平均得到的值为最终的模型输出。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"作为一个可以高度并行化的算法,RF在大数据时候大有可为。这里也对常规的随机森林算法的优缺点做一个总结。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**RF的主要优点有:**\n",
|
||||
"\n",
|
||||
"1)训练可以高度并行化,对于大数据时代的大样本训练速度有优势。个人觉得这是的最主要的优点。\n",
|
||||
"\n",
|
||||
"2)由于可以随机选择决策树节点划分特征,这样在样本特征维度很高的时候,仍然能高效的训练模型。\n",
|
||||
"\n",
|
||||
"3)在训练后,可以给出各个特征对于输出的重要性\n",
|
||||
"\n",
|
||||
"4)由于采用了随机采样,训练出的模型的方差小,泛化能力强。\n",
|
||||
"\n",
|
||||
"5)相对于Boosting系列的Adaboost和GBDT, RF实现比较简单。\n",
|
||||
"\n",
|
||||
"6)对部分特征缺失不敏感。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"随机森林的准确率可以和adaboost相媲美,但是对错误和离群点更鲁棒。\n",
|
||||
"\n",
|
||||
"随机森林中树的个数增加,森林的泛化误差收敛,因此过拟合不是问题。\n",
|
||||
"\n",
|
||||
"随机森林的准确率依赖于个体分类器的实力和他们之间的依赖性。理想情况是保持个体分类的能力而不提高他们之间的相关性。\n",
|
||||
"\n",
|
||||
"随机森林对每次划分所考虑的属性数目很敏感。通常选取$log_2^d+1$个属性。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**RF的主要缺点有:**\n",
|
||||
"\n",
|
||||
"1)在某些噪音比较大的样本集上,RF模型容易陷入过拟合。\n",
|
||||
"\n",
|
||||
"2)取值划分比较多的特征容易对RF的决策产生更大的影响,从而影响拟合的模型的效果。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"# AdaBoost"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"AdaBoost是由Freund与Schapire提出来解决二分类问题$y∈\\{1,-1\\} $,其定义损失函数为指数损失函数:"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"$$L(y,f(x))=exp(−yf(x)) $$"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"则整个样本集(n个样本)的整体损失函数,或者叫目标函数为"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"$$L(y,f(x))=\\frac{1}{n}\\sum_{i=1}^nexp(−y_if(x_i)) $$"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"我们来看看是如何根据损失函数推导出模型系数$α_m$的。\n",
|
||||
"\n",
|
||||
"由于多个基分类器总是依次出现,所以我们不会当所有分类器出现以后再计算每个分类器的权重,而是每次出现一个基分类器,我们就根据损失函数,计算当前分类器的权重。\n",
|
||||
"\n",
|
||||
"(每个分类器的权重还会影响下一个分类器的样本权重,所以必然是每训练出一个分类器,就计算一个分类器的权重)。\n",
|
||||
"\n",
|
||||
"关于为什么要使用指数损失,可以参考:https://www.cnblogs.com/willnote/p/6801496.html 或者 https://blog.csdn.net/thriving_fcl/article/details/50877957\n"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"根据加型模型(additive model),第m轮的分类函数"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"$$f_m(x)=f_{m−1}(x)+α_m G_m (x) $$"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"其中,$α_m$为基分类器$G_m(x)$的组合系数。AdaBoost采用前向分布(forward stagewise)这种贪心算法最小化损失函数,求解子模型的$α_m$"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"$$α_m =\\frac{1}{2} log\\frac{1−e_m}{e_m}$$"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"其中,$e_m$为$G_m(x)$的加权分类误差率\n",
|
||||
"$$e_m = \\frac {\\sum_{i=1}^N w_i^{(m)} I(y_i \\ne G(x_i))} {\\sum_{i=1}^N w_i^{(m)}}$$"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"第$m+1$轮的训练数据集权值分布\n",
|
||||
"$D _{m+1} =(w_{m+1},1 ,⋯,w_{m+1},i ,⋯,w_{m+1},N )$\n",
|
||||
"\n",
|
||||
"$$w_{m+1,i} =\\frac{w_{m,i}}{Z_m} exp(−α_my_iG_m (x_i)) $$\n",
|
||||
"\n",
|
||||
"其中,$Z_m$为规范化因子\n",
|
||||
"\n",
|
||||
"$$Z_m =\\sum_{i=1}^N w_{m,i} ∗exp(−α_m y_i G_m (x_i )) $$\n",
|
||||
"\n",
|
||||
"则得到最终分类器\n",
|
||||
"\n",
|
||||
"$$sign(f(x))=sign(\\sum_{m=1}^M α_m G_m (x)) $$\n",
|
||||
"\n",
|
||||
"$α_m$是$e_m$的单调递减函数,特别地,当$e_m ≤0.5$时,$α_m$ ≥0;当$e_m >12 $时,即基分类器不满足弱可学习的条件(比随机猜测好),则应该停止迭代。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"具体算法流程如下:\n",
|
||||
"\n",
|
||||
"$D_1 (i)=1/N$ %初始化权重分布\n",
|
||||
"\n",
|
||||
" for m=1,⋯,M m=1,⋯,M:\n",
|
||||
" \n",
|
||||
" learn base classifier $G_m(x)$;\n",
|
||||
" \n",
|
||||
" if $e_m>0.5$ then break;\n",
|
||||
" \n",
|
||||
" update $α_m$and $D_{m+1}$;\n",
|
||||
" \n",
|
||||
"end for"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"在算法第4步,学习过程有可能停止,导致学习不充分而泛化能力较差。\n",
|
||||
"\n",
|
||||
"因此,可采用“重采样”(re-sampling)避免训练过程过早停止;即抛弃当前不满足条件的基分类器,基于重新采样的数据训练分类器,从而获得学习“重启动”机会。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"AdaBoost能够自适应(addaptive)地调整样本的权值分布,将分错的样本的权重设高、分对的样本的权重设低;所以被称为“Adaptive Boosting”。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"sklearn的AdaBoostClassifier实现了AdaBoost,默认的基分类器是能fit()带权值样本的DecisionTreeClassifier。"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"下面是$α_m$和$G_m (x) $的推导过程,不喜欢的可以直接跳过去"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"----------\n",
|
||||
"损失函数已知为下面的公式\n",
|
||||
"$$L(y,f(x))=\\frac{1}{n}\\sum_{i=1}^nexp(−y_if(x_i)) $$\n",
|
||||
"\n",
|
||||
"我们的目标是求使得到的$α_m$和$G_m(x)$令$L(y,f(x))$最小,即:\n",
|
||||
"\n",
|
||||
"$$(\\alpha_{m},G_{m}(x))=\\underset{\\alpha_{m},G_{m}}{arg\\ min}\\sum_{i=1}^{n}e^{-y_{i}(f_{m-1}(x)+\\alpha_{m}G_{m}(x))}\\\\\n",
|
||||
"=\\underset{\\alpha_{m},G_{m}}{arg\\ min}\\sum_{i=1}^{n}\\bar{w}_{mi}e^{-y_{i}\\alpha_{m}G_{m}(x)}\\\\\n",
|
||||
"G_{m}(x)^{*}=\\underset{G_{m}(x)}{arg\\ min}\\sum_{i=1}^{n}\\bar{w}_{mi}I(y_{i}\\neq G_{m}(x))$$\n",
|
||||
"\n",
|
||||
"其中,$\\bar{w}_{mi}=e^{-y_{i}f_{m-1}(x)}$。因为$\\bar{w}_{mi}$既不依赖于$α_m$也不依赖于$G_m(x)$,所以与最小化无关。但它依赖于$f_{m−1}(x)$,会随着每一轮迭代而发生变化。第二个式子为令指数损失函数最小的$G_m(x)∗$,其中$I(⋅)$为指示函数,此$G_m(x)∗$使第$m$轮加权训练数据分类的误差率得到了最小值。接下来我们对上边的第一个式子的右边进行一下简单变形:\n",
|
||||
"\n",
|
||||
"$$\\sum_{i=1}^{n}\\bar{w}_{mi}e^{y_{i}\\alpha_{t}G_{t}(x_{i})}\\\\\n",
|
||||
"=\\sum_{y_{i}=G_{t}(x_{i})}\\bar{w}_{mi}e^{-\\alpha_{m}}+\\sum_{y_{i}\\neq G_{m}(x_{i})}\\bar{w}_{mi}e^{\\alpha_{m}}\\\\\n",
|
||||
"=(e^{\\alpha_{m}}-e^{-\\alpha_{m}})\\sum_{i=1}^{n}\\bar{w}_{mi}I(y_{i}\\neq G_{m}(x_{i}))+e^{-\\alpha_m}\\sum_{i=1}^{n}\\bar{w}_{mi}$$\n",
|
||||
"\n",
|
||||
"将上式对$α_m$求导并令导数为0,即可解得:\n",
|
||||
"$$\\alpha_{m}^{*}=\\frac{1}{2}log\\frac{1-e_{m}}{e_{m}}$$\n",
|
||||
"\n",
|
||||
"上式即之前例子中所用到的$α_m$的更新公式,其中,$e_m$为分类误差率:\n",
|
||||
"\n",
|
||||
"$$e_{m}=\\frac{\\sum_{i=1}^{n}\\bar{w}_{mi}I(y_{i}\\neq G_{m}(x_{i}))}{\\sum_{i=1}^{n}\\bar{w}_{mi}}\\\\\n",
|
||||
"=\\sum_{i=1}^{n}w_{mi}I(y_{i}\\neq G_{m}(x_{i}))$$\n",
|
||||
"\n",
|
||||
"\n",
|
||||
"----------"
|
||||
]
|
||||
},
|
||||
{
|
||||
"cell_type": "markdown",
|
||||
"metadata": {},
|
||||
"source": [
|
||||
"**算法案例代码实现:**\n",
|
||||
"\n",
|
||||
"https://github.com/626626cdllp/data-mining/tree/master/ensemble-learning/adaboost"
|
||||
]
|
||||
}
|
||||
],
|
||||
"metadata": {
|
||||
"kernelspec": {
|
||||
"display_name": "Python 3",
|
||||
"language": "python",
|
||||
"name": "python3"
|
||||
},
|
||||
"language_info": {
|
||||
"codemirror_mode": {
|
||||
"name": "ipython",
|
||||
"version": 3
|
||||
},
|
||||
"file_extension": ".py",
|
||||
"mimetype": "text/x-python",
|
||||
"name": "python",
|
||||
"nbconvert_exporter": "python",
|
||||
"pygments_lexer": "ipython3",
|
||||
"version": "3.6.9"
|
||||
}
|
||||
},
|
||||
"nbformat": 4,
|
||||
"nbformat_minor": 4
|
||||
}
|
||||
File diff suppressed because one or more lines are too long
Loading…
Reference in New Issue
Block a user