mirror of
https://github.com/tencentmusic/cube-studio.git
synced 2024-12-09 06:00:12 +08:00
210 lines
13 KiB
Plaintext
210 lines
13 KiB
Plaintext
|
|
{
|
|||
|
|
"cells": [
|
|||
|
|
{
|
|||
|
|
"cell_type": "markdown",
|
|||
|
|
"metadata": {},
|
|||
|
|
"source": [
|
|||
|
|
"# 1. BIRCH概述\n",
|
|||
|
|
"\n",
|
|||
|
|
"\n",
|
|||
|
|
" BIRCH的全称是利用层次方法的平衡迭代规约和聚类(Balanced Iterative Reducing and Clustering Using Hierarchies),名字实在是太长了,不过没关系,其实只要明白它是用层次方法来聚类和规约数据就可以了。\n",
|
|||
|
|
" \n",
|
|||
|
|
" 刚才提到了,BIRCH只需要单遍扫描数据集就能进行聚类,那它是怎么做到的呢?\n",
|
|||
|
|
"\n",
|
|||
|
|
" BIRCH算法利用了一个树结构来帮助我们快速的聚类,这个数结构类似于平衡B+树,一般将它称之为聚类特征树(Clustering Feature Tree,简称CF Tree)。这颗树的每一个节点是由若干个聚类特征(Clustering Feature,简称CF)组成。\n",
|
|||
|
|
" \n",
|
|||
|
|
" 从下图我们可以看看聚类特征树是什么样子的:树中的每个节点(包括叶子节点)都有若干个CF,而内部节点的CF有指向孩子节点的指针,所有的叶子节点用一个双向链表链接起来。\n",
|
|||
|
|
"\n",
|
|||
|
|
"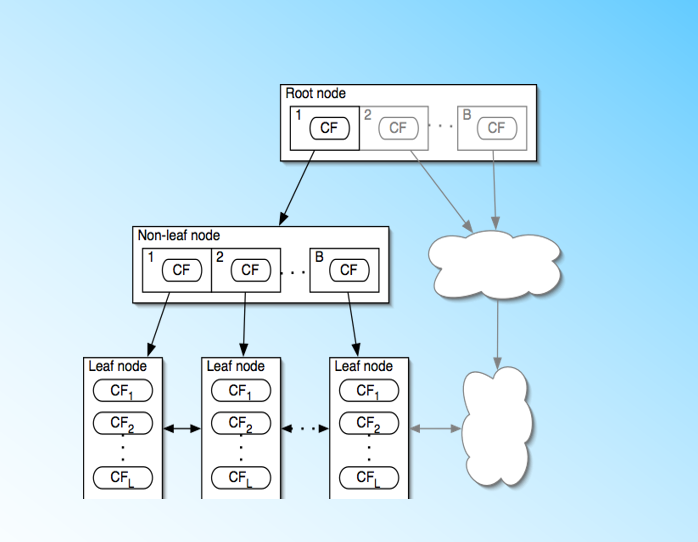\n",
|
|||
|
|
"\n",
|
|||
|
|
"\n",
|
|||
|
|
" 有了聚类特征树的概念,我们再对聚类特征树和其中节点的聚类特征CF做进一步的讲解。\n",
|
|||
|
|
" \n",
|
|||
|
|
" \n",
|
|||
|
|
"**树中的每个节点都对应一个簇(或者叫聚类)。子节点对应的簇是父节点对应的簇的子簇,所以BIRCH算法算是基于层次的聚类算法。**"
|
|||
|
|
]
|
|||
|
|
},
|
|||
|
|
{
|
|||
|
|
"cell_type": "markdown",
|
|||
|
|
"metadata": {},
|
|||
|
|
"source": [
|
|||
|
|
"# 2. 聚类特征CF与聚类特征树CF Tree\n",
|
|||
|
|
"\n",
|
|||
|
|
"\n",
|
|||
|
|
" 在聚类特征树中,一个节点的聚类特征CF是这样定义的:每一个CF是一个三元组,可以用(N,LS,SS)表示。其中N代表了这个簇中拥有的样本点的数量,这个好理解;LS代表了这个簇中拥有的样本点各特征维度的和向量,SS代表了这个簇中拥有的样本点各特征维度的平方和。\n",
|
|||
|
|
" \n",
|
|||
|
|
" 举个例子如下图,在CF Tree中的某一个节点对应的簇中,有下面5个样本(3,4), (2,6), (4,5), (4,7), (3,8)。则它对应的N=5, LS=(3+2+4+4+3,4+6+5+7+8)=(16,30), SS =(32+22+42+42+32+42+62+52+72+82)=(54+190)=244\n",
|
|||
|
|
"\n",
|
|||
|
|
"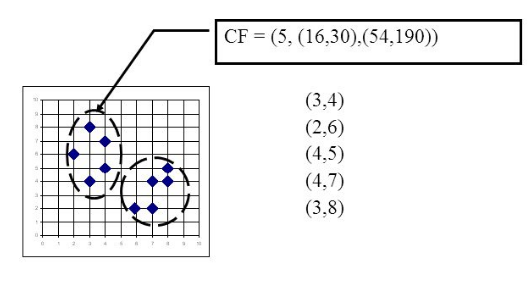\n",
|
|||
|
|
"\n",
|
|||
|
|
" CF有一个很好的性质,就是满足线性关系,也就是CF1+CF2=(N1+N2,LS1+LS2,SS1+SS2)。这个性质从定义也很好理解。\n",
|
|||
|
|
" \n",
|
|||
|
|
" 如果把这个性质放在CF Tree上,也就是说,在CF Tree中,对于每个父节点中的CF,它的(N,LS,SS)三元组的值等于它的子节点的三元组之和。如下图所示:\n",
|
|||
|
|
"\n",
|
|||
|
|
"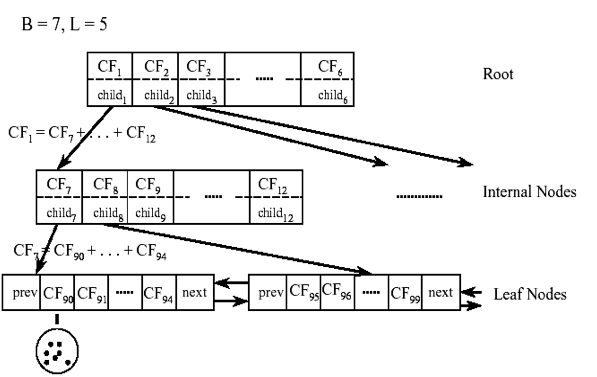\n",
|
|||
|
|
"\n",
|
|||
|
|
" 从上图中可以看出,根节点的CF1的三元组的值,可以从它指向的6个子节点(CF7 - CF12)的值相加得到。这样我们在更新CF Tree的时候,可以很高效。\n",
|
|||
|
|
"\n",
|
|||
|
|
" 对于CF Tree,我们一般有几个重要参数,第一个参数是分支因子B,表示每个非叶节点的子女的最大数目,第二个参数是阈值T,表示存储在树的叶节点中的子簇的最大直径。\n",
|
|||
|
|
" \n",
|
|||
|
|
" 也就是说,叶节点对应的子簇中的所有样本点一定要在直径小于T的一个超球体内。\n",
|
|||
|
|
" \n",
|
|||
|
|
" 有时还会定义叶节点的分支因子L,表示每个叶节点对应的子簇的最大样本个数。\n",
|
|||
|
|
" \n",
|
|||
|
|
" 对于上图中的CF Tree,限定了B=7, L=5, 也就是说内部节点最多有7个子节点,而叶子节点对应的簇最多有5个样本。"
|
|||
|
|
]
|
|||
|
|
},
|
|||
|
|
{
|
|||
|
|
"cell_type": "markdown",
|
|||
|
|
"metadata": {},
|
|||
|
|
"source": [
|
|||
|
|
"# 3. 聚类特征树CF Tree的生成\n",
|
|||
|
|
"\n",
|
|||
|
|
"\n",
|
|||
|
|
"> (注意区分:样本点、CF节点(树中的才分为节点))\n",
|
|||
|
|
"\n",
|
|||
|
|
" 下面我们看看怎么生成CF Tree。\n",
|
|||
|
|
" \n",
|
|||
|
|
" 我们先定义好CF Tree的参数: 即内部节点的最大子节点数B, 叶子节点对应的簇的最大样本数L, 叶节点对应的簇的最大样本直径阈值T。\n",
|
|||
|
|
"\n",
|
|||
|
|
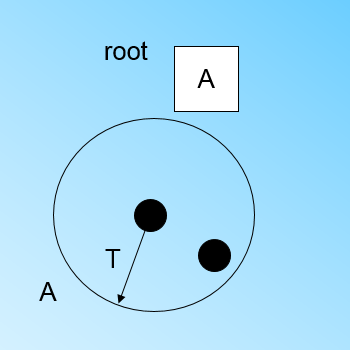
" 在最开始的时候,CF Tree是空的,没有任何样本,我们从训练集读入第一个样本点x1,将它放入一个新的节点A,这个节点的CF值中N=1,将这个新的节点作为根节点,此时的CF Tree如下图:\n",
|
|||
|
|
"\n",
|
|||
|
|
"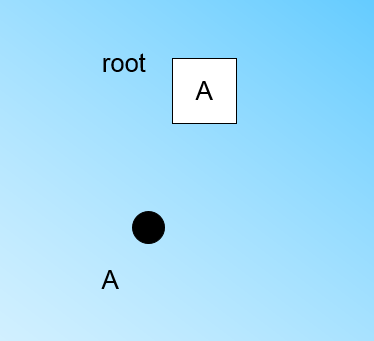"
|
|||
|
|
]
|
|||
|
|
},
|
|||
|
|
{
|
|||
|
|
"cell_type": "markdown",
|
|||
|
|
"metadata": {},
|
|||
|
|
"source": [
|
|||
|
|
"现在我们继续读入第二个样本点x2,我们发现这个样本点和第一个样本点x1,在直径为T的超球体范围内,也就是说,他们属于一个簇,我们将第二个点也加入节点A所代表的簇中,此时需要更新节点A的CF值。\n",
|
|||
|
|
"\n",
|
|||
|
|
"此时A的CF值中N=2。此时的CF Tree如下图:\n",
|
|||
|
|
"\n",
|
|||
|
|
"\n",
|
|||
|
|
"\n",
|
|||
|
|
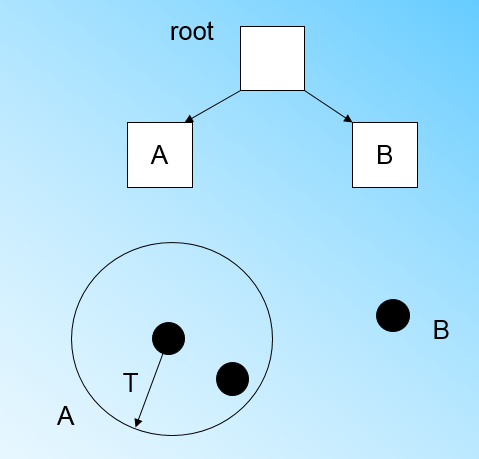
" 此时来了第三个节点x3,结果我们发现这个节点不能融入刚才前面的节点形成的超球体内,也就是说,我们需要新建一个簇来容纳x3,同时为这个簇在CF树中添加一个新的节点B。\n",
|
|||
|
|
" \n",
|
|||
|
|
" 此时根节点有两个子节点,A和B,此时的CF Tree如下图:\n",
|
|||
|
|
"\n",
|
|||
|
|
"\n",
|
|||
|
|
"\n",
|
|||
|
|
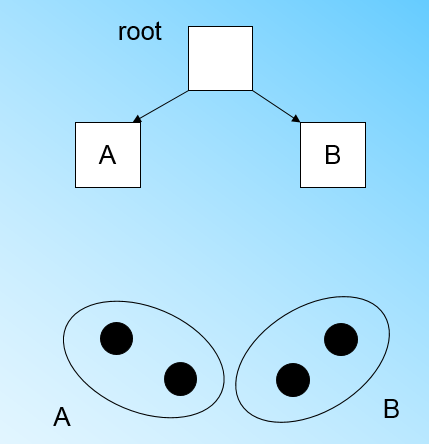
" 当来到第四个样本点x4的时候,我们发现和节点B代表的簇在直径小于T的超球体,这样更新后的CF Tree如下图:\n",
|
|||
|
|
"\n",
|
|||
|
|
"\n",
|
|||
|
|
"\n",
|
|||
|
|
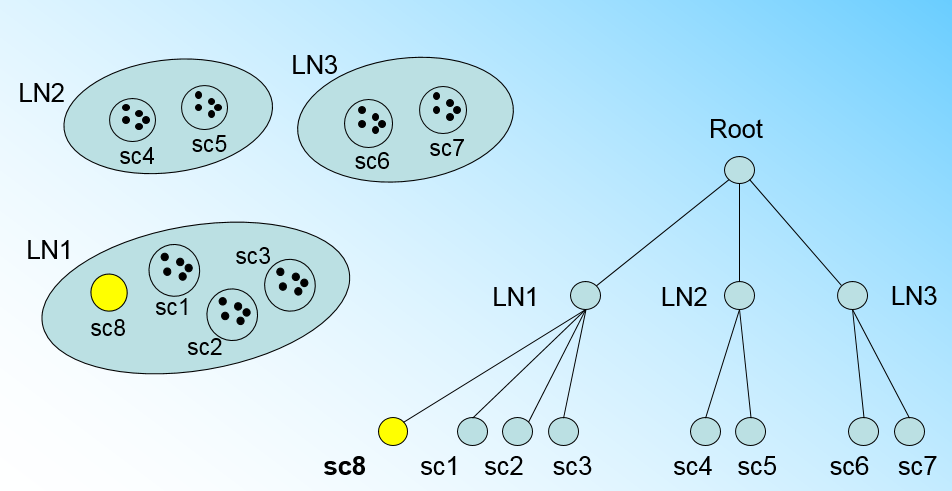
" 那个什么时候CF Tree的节点需要分裂呢?假设我们现在的CF Tree 如下图, 叶子节点LN1代表的簇有三个样本, LN2和LN3各有两个样本。我们的叶子节点的最大样本数L=3。此时一个新的样本点来了,我们发现它离LN1节点代表的簇最近,因此开始判断它是否在sc1,sc2,sc3这3个样本对应的超球体之内,但是很不幸,它不在,因此它需要建立一个新的叶子节点来容纳它。问题是我们的L=3,也就是说LN1的样本个数已经达到最大值了,不能再添加新的样本了,怎么办?此时就要将LN1叶子节点一分为二了。\n",
|
|||
|
|
"\n",
|
|||
|
|
"\n",
|
|||
|
|
"\n",
|
|||
|
|
" 我们将LN1里所有样本中,找到两个最远的样本做这两个新叶子节点的种子样本,然后将LN1节点里所有样本sc1, sc2, sc3,以及新样本点sc8划分到两个新的叶子节点上。将LN1节点划分后的CF Tree如下图:\n",
|
|||
|
|
"\n",
|
|||
|
|
"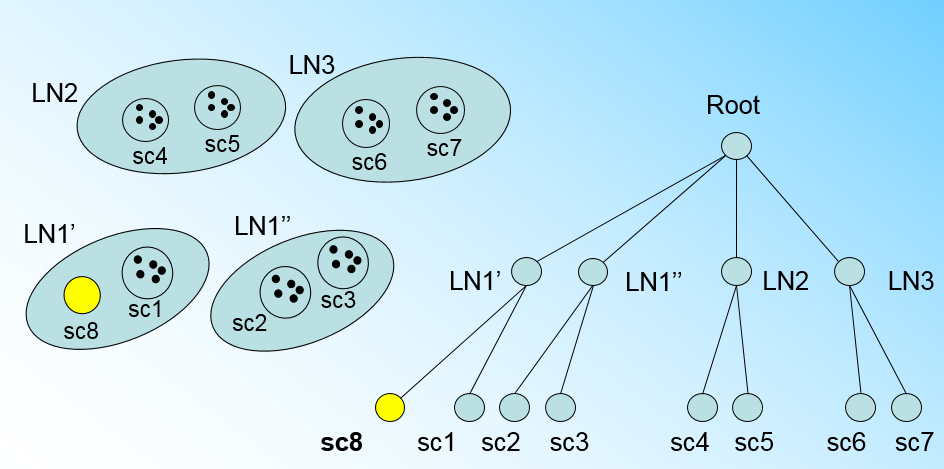\n",
|
|||
|
|
"\n",
|
|||
|
|
" 如果我们的内部节点的最大子节点数B=3,则此时叶子节点一分为二会导致根节点的最大子节点数超了,也就是说,我们的根节点现在也要分裂,分裂的方法和叶子节点分裂一样,分裂后的CF Tree如下图:\n",
|
|||
|
|
"\n",
|
|||
|
|
"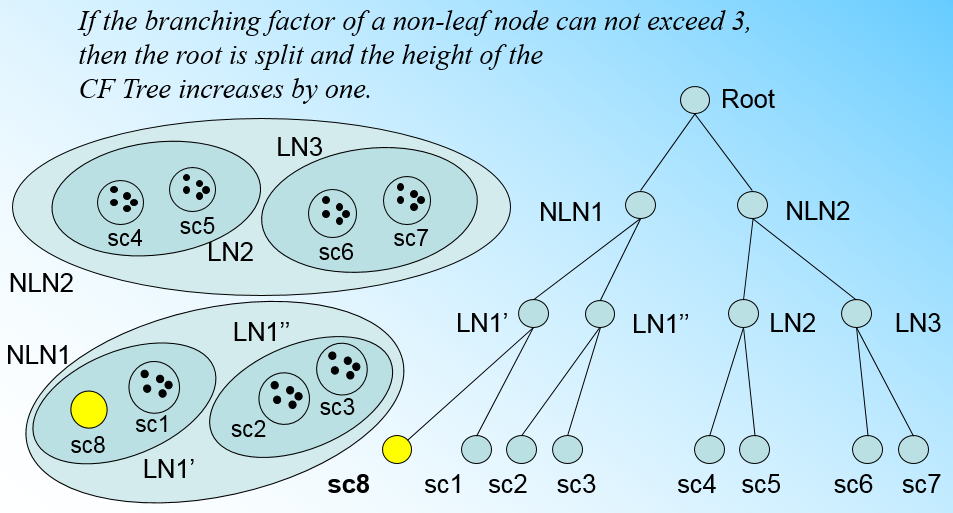"
|
|||
|
|
]
|
|||
|
|
},
|
|||
|
|
{
|
|||
|
|
"cell_type": "markdown",
|
|||
|
|
"metadata": {},
|
|||
|
|
"source": [
|
|||
|
|
"有了上面这一系列的图,相信大家对于CF Tree的插入就没有什么问题了,总结下CF Tree的插入:\n",
|
|||
|
|
"\n",
|
|||
|
|
" 1. 从根节点向下寻找和新样本距离最近的叶子节点和叶子节点里最近的样本节点\n",
|
|||
|
|
"\n",
|
|||
|
|
" 2. 如果新样本加入后,这个样本节点对应的超球体直径仍然满足小于阈值T,则将新样本点加入叶子节点对应的簇中,并更新路径上所有的树节点,插入结束。否则转入3.\n",
|
|||
|
|
" \n",
|
|||
|
|
" "
|
|||
|
|
]
|
|||
|
|
},
|
|||
|
|
{
|
|||
|
|
"cell_type": "markdown",
|
|||
|
|
"metadata": {},
|
|||
|
|
"source": [
|
|||
|
|
"\n",
|
|||
|
|
" 3.将当前叶子节点划分为两个新叶子节点,选择旧叶子节点中所有样本点中距离最远的样本点,分布作为两个新叶子节点的第一个样本节点。将其他样本和新样本按照距离远近原则放入对应的叶子节点。依次向上检查父节点是否也要分裂,如果需要,按和叶子节点分裂方式相同。\n"
|
|||
|
|
]
|
|||
|
|
},
|
|||
|
|
{
|
|||
|
|
"cell_type": "markdown",
|
|||
|
|
"metadata": {},
|
|||
|
|
"source": [
|
|||
|
|
"# 4. BIRCH算法\n",
|
|||
|
|
"\n",
|
|||
|
|
"\n",
|
|||
|
|
" 上面讲了半天的CF Tree,终于我们可以步入正题BIRCH算法,其实将所有的训练集样本建立了CF Tree,一个基本的BIRCH算法就完成了,对应的输出就是若干树节点,每个节点里的样本点就是一个聚类的簇。也就是说BIRCH算法的主要过程,就是建立CF Tree的过程。\n",
|
|||
|
|
"\n",
|
|||
|
|
" 当然,真实的BIRCH算法除了建立CF Tree来聚类,其实还有一些可选的算法步骤的,现在我们就来看看 BIRCH算法的流程。\n",
|
|||
|
|
"\n",
|
|||
|
|
" 1) 将所有的样本依次读入,在内存中建立一颗CF Tree, 建立的方法参考上一节。\n",
|
|||
|
|
"\n",
|
|||
|
|
" 2)(可选)将第一步建立的CF Tree进行筛选,去除一些异常CF节点,这些节点一般里面的样本点很少。对于一些超球体距离非常近的元组进行合并\n",
|
|||
|
|
"\n",
|
|||
|
|
" 3)(可选)利用其它的一些聚类算法比如K-Means对所有的CF元组进行聚类,得到一颗比较好的CF Tree.这一步的主要目的是消除由于样本读入顺序导致的不合理的树结构,以及一些由于节点CF个数限制导致的树结构分裂。\n",
|
|||
|
|
"\n",
|
|||
|
|
" 4)(可选)利用第三步生成的CF Tree的所有CF节点的质心,作为初始质心点,对所有的样本点按距离远近进行聚类。这样进一步减少了由于CF Tree的一些限制导致的聚类不合理的情况。\n",
|
|||
|
|
"\n",
|
|||
|
|
" 从上面可以看出,BIRCH算法的关键就是步骤1,也就是CF Tree的生成,其他步骤都是为了优化最后的聚类结果。"
|
|||
|
|
]
|
|||
|
|
},
|
|||
|
|
{
|
|||
|
|
"cell_type": "markdown",
|
|||
|
|
"metadata": {},
|
|||
|
|
"source": [
|
|||
|
|
"# 5. BIRCH算法小结\n",
|
|||
|
|
"\n",
|
|||
|
|
"\n",
|
|||
|
|
" BIRCH算法可以不用输入类别数K值,这点和K-Means,Mini Batch K-Means不同。如果不输入K值,则最后的CF元组的组数即为最终的K,否则会按照输入的K值对CF元组按距离大小进行合并。\n",
|
|||
|
|
"\n",
|
|||
|
|
" 一般来说,BIRCH算法适用于样本量较大的情况,这点和Mini Batch K-Means类似,但是BIRCH适用于类别数比较大的情况,而Mini Batch K-Means一般用于类别数适中或者较少的时候。\n",
|
|||
|
|
" \n",
|
|||
|
|
" BIRCH除了聚类还可以额外做一些异常点检测和数据初步按类别规约的预处理。\n",
|
|||
|
|
" \n",
|
|||
|
|
" 但是如果数据特征的维度非常大,比如大于20,则BIRCH不太适合,此时Mini Batch K-Means的表现较好。\n",
|
|||
|
|
"\n",
|
|||
|
|
" 对于调参,BIRCH要比K-Means,Mini Batch K-Means复杂,因为它需要对CF Tree的几个关键的参数进行调参,这几个参数对CF Tree的最终形式影响很大。\n",
|
|||
|
|
"\n",
|
|||
|
|
" 最后总结下BIRCH算法的优缺点:\n",
|
|||
|
|
"\n",
|
|||
|
|
" BIRCH算法的主要优点有:\n",
|
|||
|
|
"\n",
|
|||
|
|
" 1) 节约内存,所有的样本都在磁盘上,CF Tree仅仅存了CF节点和对应的指针。\n",
|
|||
|
|
"\n",
|
|||
|
|
" 2) 聚类速度快,只需要一遍扫描训练集就可以建立CF Tree,CF Tree的增删改都很快。\n",
|
|||
|
|
"\n",
|
|||
|
|
" 3) 可以识别噪音点,还可以对数据集进行初步分类的预处理\n",
|
|||
|
|
"\n",
|
|||
|
|
" BIRCH算法的主要缺点有:\n",
|
|||
|
|
"\n",
|
|||
|
|
" 1) 由于CF Tree对每个节点的CF个数有限制,导致聚类的结果可能和真实的类别分布不同.\n",
|
|||
|
|
"\n",
|
|||
|
|
" 2) 对高维特征的数据聚类效果不好。此时可以选择Mini Batch K-Means\n",
|
|||
|
|
"\n",
|
|||
|
|
" 3) 如果数据集的分布簇不是类似于超球体,或者说不是凸的,则聚类效果不好。\n"
|
|||
|
|
]
|
|||
|
|
}
|
|||
|
|
],
|
|||
|
|
"metadata": {
|
|||
|
|
"kernelspec": {
|
|||
|
|
"display_name": "Python 3",
|
|||
|
|
"language": "python",
|
|||
|
|
"name": "python3"
|
|||
|
|
},
|
|||
|
|
"language_info": {
|
|||
|
|
"codemirror_mode": {
|
|||
|
|
"name": "ipython",
|
|||
|
|
"version": 3
|
|||
|
|
},
|
|||
|
|
"file_extension": ".py",
|
|||
|
|
"mimetype": "text/x-python",
|
|||
|
|
"name": "python",
|
|||
|
|
"nbconvert_exporter": "python",
|
|||
|
|
"pygments_lexer": "ipython3",
|
|||
|
|
"version": "3.6.9"
|
|||
|
|
}
|
|||
|
|
},
|
|||
|
|
"nbformat": 4,
|
|||
|
|
"nbformat_minor": 4
|
|||
|
|
}
|